БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

Прежде чем сформулировать теорию, описывающую статистические закономерности, следует разумно ограничить сами требования к теории. Именно, задачей теории должно являться вычисление не точных значений различных физических величин для макроскопических тел, а средних значений этих величин по времени. Рассмотрим, например, молекулы, находящиеся в некотором выделенном в газе достаточно большом — макроскопическом — объёме. Число таких молекул с течением времени будет меняться из-за их движения, и его можно было бы найти точно, если были бы известны все координаты молекул во все моменты времени. В этом, однако, нет необходимости. Изменение числа молекул в объёме будет носить характер беспорядочных колебаний — флуктуаций — относительно некоторого среднего значения. При большом числе частиц в объёме эти колебания будут малы по сравнению со средним числом частиц, так что для характеристики макроскопического состояния достаточно знать именно это среднее значение.

Для уяснения характера статистических закономерностей рассмотрим ещё один простой пример. Пусть в некоторый сосуд помещено большое число зёрен двух сортов, каждого сорта поровну, и содержимое сосуда тщательно перемешано. Тогда на основании повседневного опыта можно быть уверенным, что во взятой из сосуда пробе, содержащей всё ещё большое число зёрен, будет обнаружено примерно равное число зёрен каждого сорта независимо от того, в каком порядке засыпались зёрна в сосуд. На этом примере хорошо видны два важных обстоятельства, обеспечивающих применимость статистической теории. Во первых, необходимость большого числа зёрен как во всей «системе» — сосуде с зерном, так и в выбранной для опыта «подсистеме» — пробе. (Если проба состоит всего из двух зёрен, то нередко оба будут одного сорта.) Во-вторых, ясно, что существенную роль играет сложность движения зёрен при перемешивании, обеспечивающая их равномерное распределение в объёме сосуда.

Функция распределения.Рассмотрим систему, состоящую из N частиц, для простоты считая, что частицы не имеют внутренних степеней свободы. Такая система описывается заданием 6N переменных — 3N координат q i и 3N импульсов p i , частиц [совокупность этих переменных сокращённо будет обозначаться ( р, q )]. Вычислим среднее значение по интервалу временит некоторой величины F ( р, q ), являющейся функцией этих координат и импульсов. Для этого разобьем интервал (0, t) на s равных малых отрезков D t a ( а = 1,2,....... s ). Тогда по определению

,

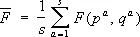или (1)

,

где q a и p a — значения координат и импульсов в моменты времени t a . В пределе s ® ¥ сумма переходит в интеграл:

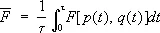(1a)

Понятие функции распределения естественным образом, возникает, если рассмотреть пространство 6 N измерений, на осях которого отложены значения координат и импульсов частиц системы; оно называется фазовым пространством. Каждому значению времени t соответствуют определённые значения всех q и р , т. е. некоторая точка в фазовом пространстве, изображающая состояние системы в данный момент времени t . Разобьем всё фазовое пространство на элементы, размер которых мал по сравнению с характерными для данного состояния системы значениями q и р , но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системы в различные моменты времени t . Тогда число таких точек в элементе объёма будет примерно пропорционально величине этого объёма dpdq . Если обозначить коэффициент пропорциональности через sw ( p, q ), то это число для элемента с центром в некоторой точке ( р, q ) запишется в виде:

da = sw ( р, q ) dpdq , (2)

где

dpdq = dp 1dq 1dp 2dq 2... dp 3Ndq 3N

— объём выбранного элемента фазового пространства. Среднее значение (1) с учётом малости этих элементов объёма можно переписать как 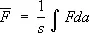, т. е.

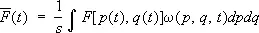(3)

(интегрирование по координатам производится по всему объёму системы, по импульсам — от —¥ до ¥). Функция w( p, q, t ) носит название функции распределения по координатами импульсам частиц. Поскольку полное число выбранных точек равно s , функция w удовлетворяет условию нормировки:

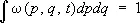(4)

Из (3) и (4) видно, что w dpdq можно рассматривать как вероятность системе находиться в элементе dpdq фазового пространства. Введённой таким образом функции распределения можно дать и др. истолкование. Для этого будем рассматривать одновременно большое число одинаковых систем и примем, что каждая точка в фазовом пространстве изображает состояние одной такой системы. Тогда усреднение по времени в (1)—(1a) можно понимать как усреднение по совокупности этих систем, или, как говорят, по статистическому ансамблю . Проведённые до сих пор рассуждения носили чисто формальный характер, т.к. нахождение функции распределения, согласно (2), требует знания всех р и q во все моменты времени, т. е. решения уравнений движения с соответствующими начальными условиями. Основным положением С. ф. является, однако, утверждение о возможности определить эту функцию из общих соображений для системы, находящейся в состоянии термодинамического равновесия. Прежде всего можно показать, исходя из сохранения числа систем при движении, что функция распределения является интегралом движения системы, т. е. остаётся постоянной, если р и q меняются в соответствии с уравнениями движения (см. Лиувилля теорема ). При движении замкнутой системы не меняется её энергия, поэтому все точки в фазовом пространстве, изображающие состояние системы в разные моменты времени, должны лежать на некоторой «гиперповерхности», соответствующей начальному значению энергии Е . Уравнение этой поверхности имеет вид;

H ( p, q ) = E ,

где Н ( р, q ) — энергия системы, выраженная через координаты и импульсы, т. е. её функция Гамильтона. Далее, движение системы из многих частиц носит крайне запутанный характер. Поэтому с течением времени точки, описывающие состояние, распределятся по поверхности постоянной энергии равномерно, подобно тому как равномерно распределяются зёрна при перемешивании в сосуде в упомянутом выше примере (см. также Эргодическая гипотеза ). Такое равномерное распределение по изоэнергетической поверхности описывается функцией распределения вида: