БСЭ БСЭ - Большая Советская Энциклопедия (СУ)

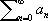(1)

умножается на некоторый множитель l n(t) так, чтобы после умножения получился сходящийся ряд

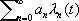(2)

с суммой d(t). При этом множители l n(t) выбираются так, чтобы при каждом фиксированном n предел l n(t) при некотором непрерывном или дискретном изменении параметра t равнялся 1. Тогда члены ряда (2) стремятся к соответствующим членам ряда (1). Если при этом d(t) имеет предел, то его называют обобщённой суммой данного ряда, соответствующей данному выбору множителей (данному методу С.). Например, если положить l n(t) = 1 При n £ t и l n(t) = 0 при n > t и брать t ® ¥ , то получится обычное понятие суммы ряда; при l n( t ) = t n для t < 1 и t ® 1 получается метод Абеля — Пуассона. Часто указывается не результат умножения членов ряда на l n(t), а соответствующие изменения частичных сумм ряда. Например, в методе средних арифметических Чезаро полагают

,

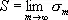где

, .

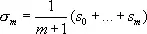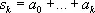Этот метод соответствует выбору l n ( m ) = ( m - n + 1)/( m + 1) при n £ m и l n ( m ) = 0 при n > m . Если положить

, ,

, ,

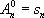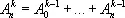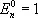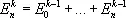и если существует 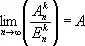, то говорят, что ряд суммируется к А методом Чезаро k -го порядка. С ростом k возрастает сила метода Чезаро, то есть расширяется множество рядов, суммируемых этим методом. Всякий ряд, суммируемый методом Чезаро какого-либо порядка, суммируется и методом Абеля — Пуассона и притом к той же сумме. Например, ряд 1— 1 + 1 —... + (—1) n-1+... суммируется методом Абеля — Пуассона к значению 1/ 2, так как

, .

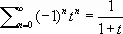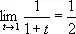Метод Чезаро даёт то же значение, так как

s 2n= 1, s 2n+l= 0, s 2n= ( n + 1)/(2 n + 1),

s 2n+1= 1/ 2, .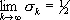

Методы Чезаро и Абеля — Пуассона применяются в теории тригонометрических рядов для нахождения функции по её ряду Фурье, так как ряд Фурье любой непрерывной функции суммируется к этой функции методом Чезаро первого порядка, а тем самым и методом Абеля — Пуассона. В 1901 Г. Ф. Вороной предложил метод С., частными случаями которого являются все методы Чезаро. Пусть p n ³ 0 , p 0= 0 , 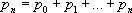; обобщённой суммой ряда, по Вороному, называется предел

.

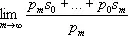Метод Вороного регулярен, если

.

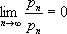В 1911 немецкий математик О. Теплиц нашёл необходимые и достаточные условия, которым должна удовлетворять треугольная матрица || а тn || (где а тn = 0 при n > m ) для того, чтобы метод С., определяемый формулой 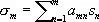, 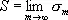был регулярен. Польский математик Х. Штейнхауз обобщил эти условия на случай квадратных матриц.

В теории аналитических функций важную роль играет метод суммирования Бореля, позволяющий аналитически продолжить функцию, заданную степенным рядом, за границу круга сходимости. Важный метод С. тригонометрических рядов был предложен С. Н. Бернштейном и немецким математиком В. Рогозинским. Бернштейн использовал этот метод для получения сходящихся интерполяционных процессов.

Теория С. расходящихся интегралов аналогична теории С. расходящихся рядов. Например, если интеграл

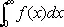
расходится и существует предел

,

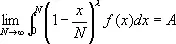то говорят, что первый интеграл суммируем к А методом Чезаро порядка l.

Лит.: Харди Г., Расходящиеся ряды, пер. с англ., М., 1951; Зигмунд А., Тригонометрические ряды, пер. с англ., [2 изд.], т. 1—2, М., 1965; Титчмарт Е., Введение в теорию интегралов Фурье, пер. с англ., М.— Л., 1948; Вари Н. К., Тригонометрические ряды, М., 1961.

Сумми'рования блок, суммирующее устройство, аналоговое вычислительное устройство, на выходе которого образуется величина, пропорциональная сумме входных величин (сигналов). Существуют механические С. б. — преимущественно для суммирования линейных ( логарифмическая линейка ) и угловых ( дифференциальный механизм ) перемещений; электромеханические С. б., в которых входные и выходные величины представляют собой механические перемещения, а суммирование выполняется с использованием законов электрических цепей (в частности, Кирхгофа правил ); электрические С. б., в которых суммируются токи или напряжения. Наибольшее распространение в электронных аналоговых вычислительных машинах получили С. б. с суммированием по току, которые для повышения точности, увеличения мощности и амплитуды выходного сигнала дополняются операционными усилителями (см. Решающий усилитель ) .

Сумми'руемая фу'нкция,функция, к которой приложимо введённое А. Лебегом понятие интеграла, то есть для которой интеграл Лебега, взятый по данному множеству, конечен. Функции эти, называемые также интегрируемыми по Лебегу, необходимо должны быть измеримыми (по Лебегу). Функция с суммируемым квадратом — измеримая функция, квадрат которой есть С. ф.

Суммово'й тон, комбинационный тон с частотой w 1+ w 2, возникающий в нелинейной акустической системе при воздействии на неё двух звуковых колебаний с частотами w 1и w 2(см. также Комбинационные колебания ) .