БСЭ БСЭ - Большая Советская Энциклопедия (ТЕ)

В тензорном анализе рассматриваются не только прямоугольные или аффинные, но и произвольные (достаточное число раз дифференцируемые) криволинейные координаты x i. В окрестности каждой точки эти координаты можно заменить аффинными координатами. В качестве базисных векторов этих аффинных координат надо взять частные производные 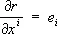радиус-вектора r в точке Р.

Тогда скалярные произведения e ie j, будут равны значениям компонент метрического тензора g ij в точке Р, с помощью которого длина бесконечно малого вектора 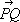, , 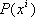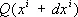выражается формулой 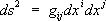. Поэтому метрика в криволинейной и прямолинейной системах координат совпадает с точностью до бесконечно малых высшего порядка. Тем самым в каждой точке пространства вводится своя (локальная) система аффинных координат, относительно которой и задаются компоненты тензорного поля в этой точке. При переходе от одной системы криволинейных координат ( x’,..., x n ) к другой ( y’,..., y n ) локальная система координат в каждой точке меняется, причём базисные векторы преобразуются по формулам 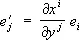. Иными словами, коэффициенты линейного преобразования 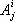будут различными в разных точках и равны 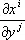; точно так же матрица 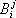состоит из выражений 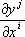. Поэтому тензорным полем относительно криволинейных координат. называют совокупность функций 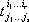, заданных в каждой точке области для системы криволинейных координат и преобразующихся при переходе от одной системы криволинейных координат к другой по формулам (2), где положено 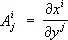, 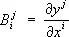. В рассматриваемом случае частные производные компонент поля по координатам x i уже не образуют тензорного поля. Это объясняется тем, что при переходе от одной точки к другой изменяются не только компоненты тензора, но и локальная координатная система, к которой этот тензор относится. Поэтому при определении изменения тензора надо учитывать не только изменение компонент тензора при переходе от точки Р ( xi ) к бесконечно близкой ей точке Q ( x’ + dx i ) , но и изменение локальной координатной системы. Иными словами, компоненты приращения тензора нельзя считать равными приращениям его компонент. Например, для векторных полей u (P), где u имеет контравариантные компоненты u; приращение векторного поля равно (с точностью до бесконечно малых высшего порядка) выражению 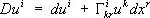. Здесь через 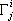обозначены так называемые символы Кристоффеля (см. Кристоффеля символ ) , связанные с метрическим тензором 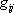соотношением

.

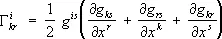Отметим, что сами символы Кристоффеля не являются тензорами. Слагаемое 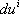учитывает зависимость компонент приращения тензора от приращения его компонент, а слагаемое 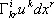— зависимость компонент приращения тензора от изменения системы координат при переходе от точки к точке.

Вектор 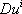называется ковариантным (или абсолютным) дифференциалом векторного поля u ( Р ) , а совокупность величин

.

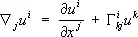— ковариантной (или абсолютной) производной этого поля. Аналогично этому ковариантная производная ковариантного векторного поля равна

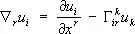
Для тензорного поля 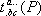ковариантная производная определяется формулой:

.

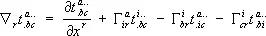Ковариантная производная тензорного поля образует тензорное поле, имеющее на одну ковариантную валентность больше, чем исходное поле. В частном случае, когда криволинейные координаты являются прямоугольными, ковариантное дифференцирование тензорных полей переходит в обычное, то есть в операцию образования поля 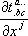. В этом случае символы Кристоффеля равны нулю.

Правила ковариантного дифференцирования (для суммы и произведения тензоров) совпадают с правилами обычного дифференцирования. Ковариантное дифференцирование перестановочно со свёртыванием. Имеет место также теорема о перестановке порядка ковариантного дифференцирования, то есть 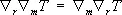. Отметим, что ковариантная производная метрического тензора 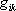равна нулю.

6. Историческая справка. Возникновение Т. и. было подготовлено в 19 в. развитием теории алгебраических форм, с одной стороны, и теории квадратичных дифференциальных форм — с другой. Исследования в области теории дифференциальных квадратичных форм были непосредственно связаны с дифференциальной геометрией: с геометрией поверхностей (К. Гаусс ) и с геометрией многомерного метрического пространства (Б. Риман ) . Современную форму Т. и. придал итальянский математик Г. Риччи-Курбастро, поэтому Т. и. иногда называется исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915—16) общей теории относительности А. Эйнштейна, математическая часть которой целиком основана на Т. и.