БСЭ БСЭ - Большая Советская Энциклопедия (ТЕ)

Т. о., одной из основных задач Т. и. является нахождение аналитических формулировок законов механики, геометрии, физики, не зависящих от выбора координатной системы.

1. Тензоры в прямоугольных координатах.Величины, которые в каждой системе прямоугольных координат задаются в 3-мерном пространстве 3 kчислами 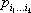( i r = 1, 2, 3) и при замене системы координат ( x 1, x 2, x 3 ) системой ( x’ 1, x’ 2, x’ 3 ) заменяются числами 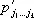по формулам:

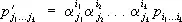, (1)

где 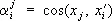, называются тензорными величинами, а определяющие их системы чисел — тензорами в прямоугольных координатах (иногда тензорами называют также и сами тензорные величины). Число k называется валентностью (рангом) тензора, числа 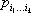— его компонентам и (координатами). Аналогичным образом определяются тензоры в пространстве любого числа измерений.

Примеры тензоров: если координаты вектора а обозначить a i ( i = 1, 2, 3), то числа а , образуют тензор первой валентности. Любым двум векторам а = { a i } и b ={ b i } соответствует тензор с компонентами p ij = a i. b j. Этот тензор называется диадой. Если a ( x 1, x 2, x 3 ) — некоторое векторное поле, то каждой точке этого поля соответствует тензор с компонентами 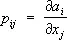. Он называется производной вектора а = {ai} по вектору r { x 1, x 2, хз } (обозначается также через 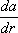). Упомянутая выше совокупность чисел J ij образует тензор второй валентности (тензор инерции).

2. Тензоры второй валентности.В приложениях Т. и. к механике, кроме тензоров первой валентности (векторов), чаще всего встречаются тензоры второй валентности.

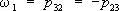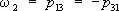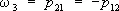
Если p ij = p ji, то тензор называется симметрическим, а если p ij= –p ji, то — кососимметрическим (антисимметрическим). Симметрический тензор имеет шесть существенных компонент, а кососимметрический — три: ; ; 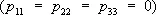. При этом компоненты w 1, w 2, w 3преобразуются как компоненты псевдовектора (см. Осевой вектор ) . Вообще псевдовекторы (угловую скорость, векторное произведение двух векторов и др.) можно рассматривать как кососимметрические тензоры второй валентности. Далее, если в любой системе координат принять 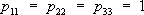, , 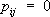, 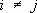то получится тензор, называемый единичным тензором. Компоненты этого тензора обозначаются при помощи Кронекера символа d ij. Тензоры инерции, напряжения, единичный тензор — симметрические. Всякий тензор единственным образом разлагается на сумму симметрических и кососимметрических тензоров. Если а ( r ) — вектор смещения частиц упругого тела при малой деформации, то симметрическая часть 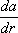называется тензором деформации; кососимметрическая часть 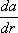соответствует псевдовектору 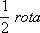(см. Вихрь векторного поля).

Тензор 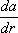является симметрическим только в том случае, когда поле а ( r ) потенциально (см. Потенциальное поле ) . Разложение тензора 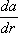на симметрические и кососимметрические части соответствует разложению относительного смещения da на чистую деформацию и на поворот тела как целого.

Инвариантами тензора называются функции от его компонент, не зависящие от выбора координатной системы. Примером инварианта является след тензора p 11 + p 22 + p 33. Так, для тензора инерции он равен удвоенному полярному моменту инерции относительно начала координат, для тензора 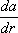— дивергенции векторного поля a ( r ) и т. д

3. Тензоры в аффинных координатах.Для многих задач приходится рассматривать тензорные величины в аффинных координатах (косоугольных координатах с различными единицами длины по разным осям). Положение одной аффинной системы координат относительно другой может быть описано двумя различными системами чисел: числами 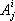равными компонентам векторов 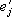. нового базиса относительно векторов 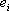старого базиса, и числами 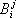, равными компонентам векторов 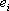относительно базиса 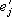. В соответствии с этим бывают тензоры различного вида: в законы преобразования одних из них входят числа 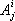, а в законы преобразования других — числа 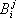. Встречаются и тензоры, в законы преобразования которых входят как числа 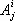, так и числа 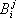. Тензоры первого вида называются ковариантными, второго — контравариантными и третьего — смешанными тензорами. Более точно, ( r + х )-валентным смешанным тензором s раз ковариантным и r раз контравариантным. называют совокупность 3 r+s чисел 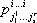, заданную в каждой системе аффинных координат и преобразующуюся при переходе от одной системы координат к другой по формулам: