БСЭ БСЭ - Большая Советская Энциклопедия (ТЕ)

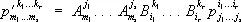
При рассмотрении прямоугольных координат не приходится различать ковариантные (нижние) и контравариантные (верхние) индексы тензора, так как для двух таких систем координат .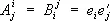

Коэффициенты уравнения поверхности второго порядка 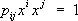образуют ковариантный тензор валентности 2, а элементы 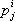матрицы линейного преобразования — тензор, 1 раз ковариантный и 1 раз контравариантный. Система трёх чисел x 1, x 2, x 3, преобразующихся как координаты вектора x = x ie i, образует 1 раз контравариантный тензор, а система чисел, преобразующихся как скалярное произведение x i= xe i, образует 1 раз ковариантный тензор. Относительно преобразования аффинных координат символ Кронекера 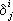является смешанным тензором (поэтому, в отличие от пункта 2, здесь пишут один индекс сверху, другой — снизу). Совокупность чисел g ij= e ie j, где e i — векторы базиса, образует тензор, называемый ковариантным метрическим тензором. Длина любого вектора пространства х = xiei равна 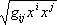, а скалярное произведение двух векторов х и у равно g ijx iy j. Совокупность величин g ij таких, что 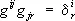, образует тензор, который называется контравариантным метрическим тензором.

Дословно, так же как и в трёхмерном пространстве, определяются тензоры в n -мерном пространстве. Важным примером тензоров в n -мерном пространстве являются совокупности компонент поливекторов.

Порядок следования индексов существенным образом входит в определение тензора, то есть при перестановке индексов компоненты тензора, вообще говоря, меняются. Тензор называется симметрическим по данной совокупности индексов (одного и того же уровня), если при перестановке любых двух индексов этой совокупности он не меняется. Если же при такой перестановке компоненты тензора меняют знак, то он называется кососимметрическим по этой совокупности индексов. В более общем смысле условием симметрии тензора называют любую инвариантную линейную зависимость между его компонентами.

4. Действия над тензорами.Существуют четыре основные операции над тензорами: сложение тензоров, умножение тензоров, свёртывание тензоров по двум или более индексам и перестановка индексов тензора. Так как тензор задаётся своими компонентами в различных системах координат, то действия над тензорами задаются формулами, выражающими в каждой системе координат компоненты результата действия через компоненты тензоров, над которыми производятся действия. При этом формулы должны быть такими, чтобы в результате выполнения действия получился тензор.

а) Сложение тензоров. Суммой двух тензоров 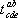и 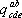одинакового строения (то есть имеющих одинаковое число верхних и нижних индексов) называется тензор с компонентами

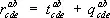
б) Умножение тензоров. Произведением двух тензоров 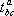и 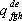(быть может различного строения) называется тензор с компонентами 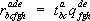. Произведение тензоров, вообще говоря, зависит от порядка сомножителей. Если один из тензоров имеет нулевую валентность (то есть является скалярной величиной l) , то умножение его на другой тензор 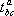сводится к умножению всех компонент тензора 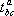на число l.

в) Свёртывание тензора. Результатом свёртывания тензора 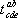по индексам а и d (верхнему и нижнему) называется тензор 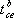, компоненты которого равны 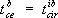. (здесь производится суммирование по индексу i). Например, след матрицы 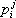является результатом свёртывания её по индексам i и j , бискалярное произведение 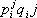тензоров 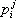и 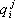. равно результату свёртывания их произведения по всем индексам. При полном свёртывании тензора (по всем индексам) получается инвариант.

г) Перестановка индексов. Пусть компоненты тензора 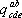выражаются через компоненты тензора 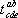формулой 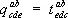. Тогда говорят, что 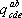получился из 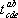перестановкой индексов с и е. При этом переставляться могут только индексы одного и того же уровня.

5. Тензорный анализ.В приложениях приходится обычно рассматривать не отдельные тензоры, а тензорные поля. Например, при изучении упругой деформации рассматривают тензоры деформации и напряжений во всех точках тела. Если в пространстве задана прямоугольная система координат, то тензорное поле Т ( Р ) можно рассматривать как совокупность функций 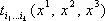, заданных в каждой точке Р ( х 1, x 2, x 3 ) области и преобразующихся при переходе от одной системы прямоугольных координат к другой по формулам вида (1). В этом случае частные производные компонент тензора по координатам 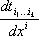образуют также тензор, валентность которого на единицу выше валентности исходного тензора. Например, при дифференцировании скалярного поля получается поле градиента, при дифференцировании поля градиента — поле симметрического тензора второй валентности: 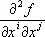и т. д.