БСЭ БСЭ - Большая Советская Энциклопедия (ФО)

Элементы взаимного ориентирования позволяют установить снимки в то положение относительно друг друга, которое они занимали при фотографировании объекта. В этом случае каждая пара соответственных лучей, например S 1m1и S 2m2 , пересекается и образует точку ( m ) модели. Совокупность лучей, принадлежащих снимку, называется связкой, а центр проекции – S 1или S 2– вершиной связки. Масштаб модели остаётся неизвестным, т.к. расстояние S 1 S 2между вершинами связок выбирается произвольно. Соответственные точки стереопары m 1и m 2находятся в одной плоскости, проходящей через базис S 1 S 2. Поэтому

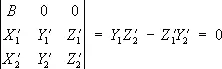(6)

Полагая, что приближённые значения элементов взаимного ориентирования известны, можно представить уравнение (6) в линейном виде:

a da 1’ + b da 2’ + с dw 2’ + d dc 1’ + e dc 2’ + l = V , (7)

где da 1’,... e dm 2’ – поправки к приближённым значениям неизвестных, а,..., е – частные производные от функции (6) по переменным a 1’ ,... c 2’, l – значение функции (6), вычисленное по приближённым значениям неизвестных. Для определения элементов взаимного ориентирования измеряют координаты не менее пяти точек стереопары, а затем составляют уравнения (7) и решают их способом последовательных приближений. Координаты точек модели вычисляют по формулам (4), выбрав произвольно длину базиса В и полагая X s 1= Y s 1 = Z s 1 = 0, B X = В, B Y = B Z = 0 . При этом пространственные координаты точек m 1и m 2находят по формулам (2), а направляющие косинусы – по формулам (3): для снимка P 1по элементам a 1’, w 1’ = 0, c 1’ , а для снимка P 2по элементам a 2’ , w 2’ , c 2’ .

По координатам X’ Y’ Z’ точки модели определяют координаты точки объекта:

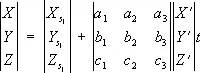, (8)

где t – знаменатель масштаба модели. Направляющие косинусы получают по формулам (3), подставляя вместо углов a, w и c продольный угол наклона модели x, поперечный угол наклона модели h и угол поворота модели q.

Для определения семи элементов внешнего ориентирования модели – 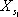, , 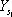, 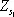x, h, q, t – составляют уравнения (8) для трёх или более опорных точек и решают их. Координаты опорных точек находят геодезическими способами или методом фототриангуляции. Совокупность точек объекта, координаты которых известны, образует цифровую модель объекта, служащую для составления карты и решения различных инженерных задач, например для изыскания оптимальной трассы дороги. Кроме аналитических методов обработки снимков, применяются аналоговые, основанные на использовании фотограмметрических приборов – фототрансформатора, стереографа, стереопроектора и др.

Щелевые и панорамные фотоснимки, а также снимки, полученные с применением радиолокационных, телевизионных, инфракрасных-тепловых и других съёмочных систем, существенно расширяют возможности Ф., особенно при космических исследованиях. Но они не имеют единого центра проекции, и элементы внешнего ориентирования их непрерывно изменяются в процессе построения изображения, что осложняет использование таких снимков для измерительных целей.

Основные достоинства фотограмметрических методов работ: большая производительность, т.к. измеряются не объекты, а их изображения; высокая точность благодаря применению точных аппаратов и инструментов для получения и измерения снимков, а также строгих способов обработки результатов измерений; возможность изучения как неподвижных, так и движущихся объектов; полная объективность результатов измерений; измерения выполняются дистанционным методом, что имеет особое значение в условиях, когда объекты недоступны (летящий самолёт или снаряд) или когда пребывание в зоне объекта небезопасно для человека (действующий вулкан, ядерный взрыв). Ф. широко применяется для создания карт Земли, других планет и Луны, измерения геологических элементов залегания пород и документации горных выработок, изучения движения ледников и динамики таяния снежного покрова, определения лесотаксационных характеристик, исследования эрозии почв и наблюдения за изменениями растительного покрова, изучения морских волнений и течений и выполнения подводных съёмок, изысканий, проектирования, возведения и эксплуатации инженерных сооружений, наблюдения за состоянием архитектурных ансамблей, зданий и памятников, определения в военном деле координат огневых позиций и целей и др.

Лит.: Бобир Н. Я., Лобанов А. Н., Федорук Г. Д., Фотограмметрия, М., 1974; Дробышев Ф. В., Основы аэрофотосъемки и фотограмметрии, 3 изд., М., 1973; Коншин М. Д., Аэрофотограмметрия, М., 1967; Лобанов А. Н., Аэрофототопография, М., 1971; его же, Фототопография, 3 изд., М., 1968; Дейнеко В. Ф., Аэрофотогеодезия, М., 1968; Соколова Н. А., Технология крупномасштабных аэротопографических съемок, М., 1973; Русинов М. М., Инженерная фотограмметрия, М., 1966; Rüger W., Buchholtz A., Photogrammetrie, 3 Aufl, B., 1973; Manual of photogrammetry, v. 1–2, Menasha, 1966; Bonneval Н., Photogrammétrie générate, t. 1–4, P., 1972; Piasecki М. B., Fotogrametria, 3 wyd., Warsz., 1973.

А. Н. Лобанов.

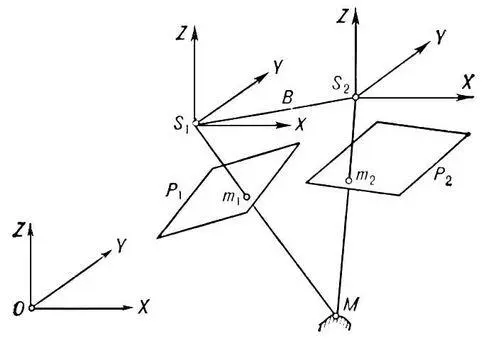
Рис. 2. к ст. Фотограмметрия.

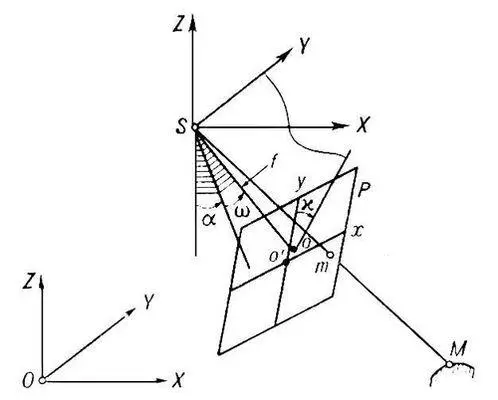
Рис. 1. к ст. Фотограмметрия.

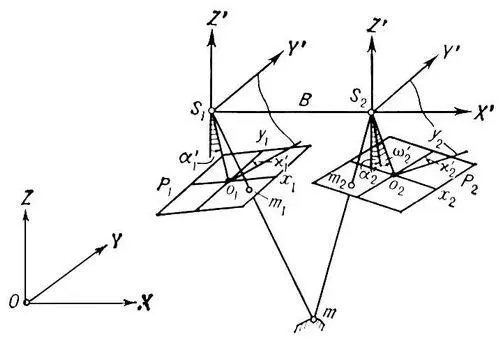
Рис. 3. к ст. Фотограмметрия.

Фотографи'ческая астрометри'я,раздел астрометрии, посвященный методам решения астрономических задач с помощью фотографий звёздного неба. К числу задач, решаемых Ф. а., относятся: измерение небесных координат звёзд, планет, искусственных небесных тел и др.; определение собственных движений небесных объектов; измерение тригонометрических параллаксов звёзд; изучение движений компонентов двойных звёзд и др.

Методы Ф. а. основаны на определении эмпирической зависимости между прямоугольными координатами некоторой группы звёзд (т. н. опорных звёзд), измеренными с помощью координатно-измерительной машины на астронегативе, и экваториальными небесными координатами этих же звезд, заимствованными из звёздного каталога. Эта зависимость позволяет по измеренным на фотоснимке прямоугольным координатам любого др. небесного объекта (звезды, планеты и т.д.) определить его экваториальные координаты. При вычислениях координат небесных светил, называемых астрометрической редукцией, принимают во внимание собственные движения опорных звёзд, вносят исправления искажений, обусловленных рефракцией света в атмосфере, годичной и суточной аберрацией света, аберрациями оптических систем и др. При астрометрической редукции широко применяется Тёрнера метод.