БСЭ БСЭ - Большая Советская Энциклопедия (ФУ)

где

.

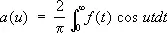Формулу (2) можно рассматривать как предельную форму ряда Фурье для функций, имеющих период 2 T , когда Т ® ¥. При этом а ( u ) и b ( u ) аналогичны коэффициентам Фурье функции f ( x ). Употребляя комплексные числа, можно заменить формулу (1) формулой

.

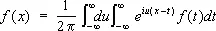Формулу (1) можно преобразовать также к виду

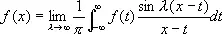(3)

(простой интеграл Фурье).

Если интегралы в формулах (2), (3) расходятся (см. Несобственные интегралы ), то во многих случаях их можно просуммировать к f ( x ) при помощи того или иного метода суммирования . При решении многих задач используются формулы Ф. и. для функций двух и большего числа переменных.

Лит.: Титчмарш Е., Введение в теорию интегралов Фурье, пер. с англ., М. — Л., 1948.

Фурье' коэффицие'нты,коэффициенты

(*)

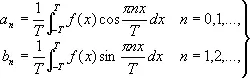разложения функции f (x) , имеющей период 2 T , в ряд Фурье (см. Фурье ряд ). Формулы (*) называют формулами Эйлера — Фурье. Непрерывная функция f ( x ) однозначно определяется своими коэффициентами Фурье. Ф. к. интегрируемой функции f ( x ) стремятся к нулю при n ® ¥, причём скорость их убывания зависит от дифференциальных свойств функции f ( x ). Например, если f ( x ) имеет k непрерывных производных, то существует такое число с , что | a n | £ c/n k , | b n | £ c/n k . Ф. к. связаны с f ( x ) также следующим неравенством:

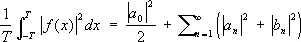
(см. Парсеваля равенство ). Ф. к. функции f ( x ) по любой нормированной ортогональной на отрезке [ а , b ] системе функций j 1( x ), j 2( x ),..., j n ( x ),... (см. Ортогональная система функций ) равны

.

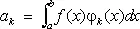Фурье' ме'тод,метод решения задач математической физики, основанный на разделении переменных. Предложен для решения задач теории теплопроводности Ж. Фурье и в полной общности сформулирован М. В. Остроградским в 1828. Решение уравнения, удовлетворяющее заданным начальным однородным и краевым условиям, ищется по Ф. м. как суперпозиция решений, удовлетворяющих краевым условиям и представимых в виде произведения функции от пространственных переменных на функцию от времени. Нахождение таких решений связано с разысканием собственных функций и собственных значений некоторых дифференциальных операторов и последующим разложением функций начальных условий по найденным собственным функциям. В частности, разложение функций в ряды и интегралы Фурье (см. Фурье ряд , Фурье интеграл ) связано с применением Ф. м. для изучения задач о колебании струны и о теплопроводности стержня. Например, изучение малых колебаний струны длины l , имеющей закрепленные концы, сводиться к решению уравнения 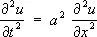при краевых условиях u (0, t ) = u ( l , t ) = 0 и начальных условиях u ( x ,0) = f ( x ); u' t ( x , 0) = F ( x ); 0 £ x £ l . Решения этого уравнения, имеющие вид X ( x ) T ( t ) и удовлетворяющие краевым условиям, выражаются формулой:

.

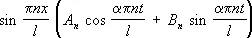Выбирая соответствующим образом коэффициенты A n и B n , можно добиться того, что функция

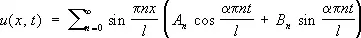
будет решением поставленной задачи.

Ряд важных проблем, связанных с применением Ф. м., был решен В. А. Стекловым .

Фурье' преобразова'ние(данной функции), функция, выражающаяся через данную функцию f ( x ) формулой:

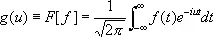, (1)

Если функция f ( x ) чётная, то её ф. п. равно

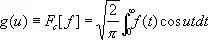(2)

(косинус-преобразование), а если f ( x ) — нечётная функция, то

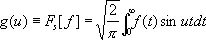(3)

(синус-преобразование). Формулы (1), (2) и (3) обратимы, т. е. для чётных функций

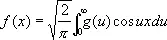, (4)

а для нечётных функций

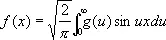. (5)

В общем случае имеет место формула

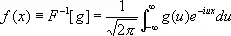. (6)

Каждой операции над функциями соответствует операция над их Ф. п., которая во многих случаях проще соответствующей операции над f ( x ). Например, Ф. п. f '( x ) является iug ( u ). Если

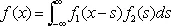, (7)

то g ( u ) = g 1 ( u ) g 2 ( u ). Для f ( x + а ) Ф. п. является e iuag ( u ), а для c 1f 1 ( x ) + c 2f 2 ( x ) — функция c 1g 1 ( u ) + c 2g 2 ( u ).

Если существует 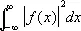, то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость ), причём

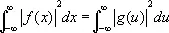(8)

(теорема Планшереля). Формула (8) является обобщением на Ф. п. формулы Парсеваля (см. Парсеваля равенство ) для рядов Фурье (см. Фурье ряд ). Физический смысл формулы (8) заключается в равенстве энергии некоторого колебания сумме энергий его гармонических компонент. Отображение F : f ( x ) ® g ( u ) является унитарным оператором в гильбертовом пространстве функций f ( x ), — ¥ < x < ¥, с интегрируемым квадратом. Этот оператор может быть представлен также в виде