БСЭ БСЭ - Большая Советская Энциклопедия (ФУ)

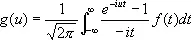. (9)

При некоторых условиях на f ( x ) справедлива формула Пуассона

,

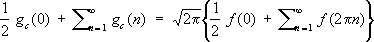находящая применение в теории тэта-функций .

Если функция f ( x ) достаточно быстро убывает, то её Ф. п. можно определить и при некоторых комплексных значениях u = v + iw . Например, если существует 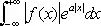, а > 0, то Ф. п. определено при | w | < а. Ф. п. при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование )

.

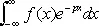
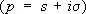Оператор Ф. п. может быть расширен на более обширные классы функций, нежели совокупность суммируемых функций [например, для функций f ( x ) таких, что (1 + | x |) –1 f ( x ) суммируема, Ф. п. определяется формулой (9)], и даже на некоторые классы обобщённых функций (т. н. медленного роста).

Имеются обобщения Ф. п. Одно из них использует различного рода специальные функции, например Бесселя функции , это направление получает завершение в теории представлений непрерывных групп . Другим является т. н. преобразование Фурье — Стилтьеса, широко применяемое, например, в теории вероятностей; оно определяется для произвольной ограниченной неубывающей функции j( x ) Стилтьеса интегралом

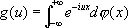(10)

и называется характеристической функцией распределения j. Для представимости функции g ( u ) в виде (10) необходимо и достаточно, чтобы при любых u 1,..., u n , x 1,...,x n было

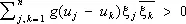
(теорема Бохнера — Хинчина).

Ф. п., первоначально возникшее в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, Ф. п. стало стандартным аппаратом квантовой теории поля , широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.

Лит.: Снеддон И., Преобразование Фурье, пер. с англ., М., 1955; Владимиров В. С., Обобщенные функции в математической физике, М., 1976.

Фурье' ряд, тригонометрический ряд , служащий для разложения периодической функции на гармонические компоненты. Если функция f ( x ) имеет период 2 T , то её Ф. р. имеет вид

,

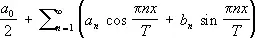где a 0 , a n , b n ( n ³ 1) — Фурье коэффициенты . В зависимости от того, в каком смысле понимаются интегралы в формулах для коэффициентов, говорят о рядах Фурье — Римана, Фурье — Лебега и т.д. Обычно рассматривают 2p-периодические функции (общий случай сводится к ним преобразованием независимого переменного).

Ф. р. представляют собой простейший класс разложений по ортогональной системе функций , а именно — по тригонометрической системе 1, cos x , sin x , cos 2 x , sin 2 x ,..., cos nx , sin nx ,..., которая обладает двумя важными свойствами: замкнутостью и полнотой. Частичные суммы Ф. р. (суммы Фурье)

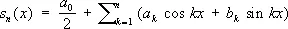
обращают в минимум интеграл

,

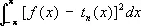где t n ( x ) — произвольный тригонометрический полином порядка £ n , а функция f ( x ) интегрируема с квадратом. При этом

,

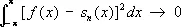
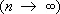так что функции f ( x ), имеющие интегрируемый квадрат, сколь угодно хорошо аппроксимируются своими суммами Фурье в смысле среднего квадратичного уклонения (см. Приближение и интерполирование функций ).

Для любой интегрируемой функции f ( x ) коэффициенты Фурье a n , b n при n ® ¥ стремятся к нулю (Б. Риман, А. Лебег). Если же функция f ( x ) несобственно интегрируема по Риману, то коэффициенты Фурье могут и не стремиться к нулю (Риман). В случае, если квадрат функции f ( x ) интегрируем, то ряд 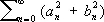сходится и имеет место равенство Парсеваля

.

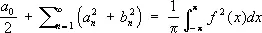Один из вариантов этой формулы был впервые указан французским математиком М. Парсевалем (1799), а общая формула (где интеграл понимается в смысле Лебега) доказана Лебегом. Обратно, для любой последовательности действительных чисел a n , b n со сходящимся рядом 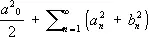существует функция с интегрируемым по Лебегу квадратом, имеющая эти числа своими коэффициентами Фурье (немецкий математик Э. Фишер, венгерский математик Ф. Рис). Для интегралов в смысле Римана эта теорема неверна.

Известно большое число признаков сходимости Ф. р., т. е. достаточных условий, гарантирующих сходимость ряда. Например, если функция f ( x ) имеет на периоде конечное число максимумов и минимумов, то её Ф. р. сходится в каждой точке (П. Дирихле ). Более общо, если f ( x ) имеет ограниченное изменение (см. Изменение функции ), то её Ф. р. сходится в каждой точке и притом равномерно на каждом отрезке, внутреннем к отрезку, на котором f ( x ) непрерывна (К. Жордан ). Если f ( x ) непрерывна и её модуль непрерывности w(d, f ) удовлетворяет условию 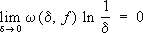, то её Ф. р. равномерно сходится (итальянский математик У. Дини, 1880).

Проблема полного исследования условий сходимости Ф. р. оказалась весьма трудной, и в этом направлении до сих пор нет окончательных результатов. Как показал Риман, сходимость или расходимость Ф. р. в некоторой точке x 0 зависит от поведения функции f ( x ) лишь в сколь угодно малой окрестности этой точки (т. н. принцип локализации для Ф. р.). Если в точке x 0 функция f ( x ) имеет разрыв первого рода, т. с. существуют различные пределы f ( x 0 — 0) и f ( x 0 + 0), и Ф. р. этой функции сходится в точке x 0 , то он сходится к значению 1/ 2{ f ( x 0 — 0) + f ( x 0 + 0)}. В частности, если Ф. р. непрерывной периодической функции f ( x ) сходится в каждой точке, то его сумма равна f ( x ).