БСЭ БСЭ - Большая Советская Энциклопедия (ХА)

Лит.: Блаватский В. Д., Харакс, в кн.: Материалы и исследования по археологии СССР, № 19, М. — Л., 1951.

Хара'ктерв математике, функция специального вида, применяемая в чисел теории и теории групп .

В теории чисел Х. называют функцию c( n ) ¹ 0, определённую для всех целых чисел n и такую, что: 1) c( nm ) = c( n )c( m ) для всех n и m , 2) существует такое целое число k (период), что c( n + k ) = c( n ) для всех n . Наименьший из положительных периодов называется основным модулем характера c, а характер с основным модулем k обозначается c( n , k ). Примерами Х. являются: 1) главный Х. по модулю k ; c( n , k ) = 0, если ( n , k ) > 1, и c( n , k ) = 1, если ( n , k ) = 1, 2) c( n , k ) = 0, если ( n , k ) > 1, c( n , k ) = 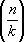, если ( n , k ) = 1, 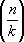— Якоби символ , k > 1 — нечётное натуральное число. Х. степени q по модулю k называется Х., равный единице для чисел и, для которых разрешимо сравнение x q º a (mod k ) (см. Степенной вычет ). Такие Х. играют важную роль в теории алгебраических чисел. Многие вопросы теории чисел (например, вопрос о распределении простых чисел) связаны с изучением функций L ( s c) = 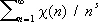(т. н. L -функций Дирихле). Частным случаем таких функций является дзета-функция x( s ), для которой Х ( n ) º 1.

Условие периодичности c( n + k ) = c( n ) позволяет трактовать характеры c( n , k ) при фиксированном k > 1 как функции, заданные на приведённой системе вычетов по модулю k , рассматриваемой как группа по умножению, и удовлетворяющие там функциональному уравнению:

c( ab ) = c( a ) c( b ). (1)

Такая трактовка понятия Х. позволяет непосредственно перенести его на любую конечную коммутативную группу G . При этом, если n — порядок, e — единица, a — произвольный элемент группы G , то [c( a )] n = c( a n ) = c( e ) = 1, т. е. c( a ) — корень n -й степени из единицы: в частности

|c( a )| º 1. (2)

Х. произвольной коммутативной группы G (не обязательно конечной) называют всякую функцию c( а ), определённую на G и удовлетворяющую условиям (1) и (2). Если G — топологическая группа, то требуют ещё, чтобы c( а ) была непрерывна.

Совокупность всех Х. группы G образует группу G 1 , относительно обыкновенного умножения Х. как функций. Если G конечна, то G 1 изоморфна G . Для бесконечных групп это уже, вообще говоря, неверно. Например, если G — группа целых чисел, то её Х. служат c( n ) = e in j, где (j — любое действительное число, приведённое по модулю 2p, так что группа Х. совпадает с группой вращений окружности. В свою очередь, группа Х. для группы вращений окружности совпадает с группой целых чисел [каждый такой Х. имеет вид: c(j) = e in j]. Эта двойственность была обобщена Л. С. Понтрягиным на широкий класс групп и применена к решению важных проблем топологии (т. н. проблем двойственности для компактов).

Лит.: Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; Чудаков Н. Г., Введение в теорию L-функций Дирихле, М. — Л., 1947; Ленг С., Алгебра, пер. с англ., М., 1968; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972.

Хара'ктер(от греч. charakter — отпечаток, признак, отличительная черта) в психологии, целостный и устойчивый индивидуальный склад душевной жизни человека, её тип, «нрав» человека, проявляющийся в отдельных актах и состояниях его психической жизни, а также в его манерах, привычках, складе ума и свойственном человеку круге эмоциональной жизни. Х. человека выступает в качестве основы его поведения и составляет предмет изучения характерологии .

Хара'ктерлитературный, образ человека, очерченный с известной полнотой и индивидуальной определённостью, через который раскрываются как обусловленный данной общественно-исторической ситуацией тип поведения (поступки, мысли, переживания, речевая деятельность), так и присущая автору нравственно-эстетическая концепция человеческого существования. Художественный Х. являет собой органическое единство общего, повторяющегося и индивидуального, неповторимого; объективного (социально-психологическая реальность человеческой жизни, послужившая прообразом для литературного Х.) и субъективного (осмысление и оценка прообраза автором). В результате Х. в искусстве предстаёт «новой реальностью», художественно «сотворённой» личностью, которая, отображая реальный человеческий тип, идеологически проясняет его. Именно концептуальность литературного образа человека отличает понятие Х. в литературоведении от значений этого термина в психологии, философии, социологии.

Представление о Х. литературного героя создаётся посредством внешних и внутренних «жестов» (в т. ч. речи) персонажа, его внешности, авторскими и иными характеристиками, местом и ролью персонажа в развитии сюжета . Соотношение в пределах произведения Х. и обстоятельств, являющихся художественным воспроизведением социально-исторической, духовно-культурной и природной среды, составляет художественную ситуацию. Противоречия между человеком и обществом, между человеком и природой, его «земной участью», а также внутреннего противоречия человеческих Х. воплощаются в конфликтах художественных.

Воспроизведение Х. в его многоплановости и динамике — специфическое свойство художественной литературы в целом (и большинства театральных и кинематографических жанров на словесно-сюжетной основе). Обращение к изображению Х. знаменует выделение литературы как искусства из синкретической, «долитературной» религиозно-публицистической словесности «библейского» или средневекового типа. Само понятие Х. формируется в Древней Греции, где впервые вполне осуществилось выделение литературно-художественного творчества в особую область духовной культуры.

Однако у древних понимание Х. как лит. категории отличалось от современного: поскольку в раскрытии идейного содержания главенствовал сюжет (событие), персонажи различались прежде всего не своими Х., а своей ролью в изображаемых событиях. В новое время утверждается иное соотношение Х. и сюжета: не факты, а «... характеры действующих лиц, благодаря которым факты осуществились, заставляют поэта избрать предпочтительнее то, а не другое событие. Только характеры священны для него» (Лессинг Г. Э., Гамбургская драматургия, М. — Л., 1936, с. 92). Понимание самостоятельного идейно-художественного значения Х. персонажа возникает уже в античной литературе; например, в «Параллельных жизнеописаниях» Плутарха герои сравниваются и по типу «судьбы», и по типу Х. Подобная характерологическая двумерность доминирует вплоть до 18 в. (по Д. Дидро — соотношение прирождённого «нрава» и «общественного положения»).