БСЭ БСЭ - Большая Советская Энциклопедия (ХА)

Х. дифференциального уравнения 2-го порядка

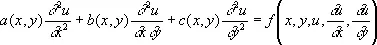(3)

были введены Г. Монжем (1784, 1795) как линии, вдоль которых удовлетворяется обыкновенное дифференциальное уравнение

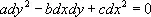. (4)

Если уравнение (3) принадлежит к гиперболическому типу, то получаются два семейства Х. с уравнениями x( x , y ) = C 1 и h( х , у ) = C 2 ( C 1, C 2— произвольные постоянные); взяв x и h за новые аргументы, можно привести уравнение (3) к виду

.

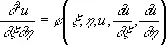Для уравнения (3) параболического типа эти семейства совпадают; если выбрать аргумент h произвольно, то уравнение (3) приведется к виду

.

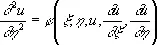Уравнение (3) эллиптического типа не имеет вещественных Х.; если записать решение уравнения (4) в виде x ± i h = C , то уравнение (3) преобразуется к виду

.

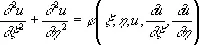Значения решения и вдоль Х. и значения 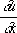и 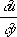в какой-либо её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод Х. решения краевых задач для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения u , и 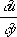, заданные на линии, не являющейся Х., определяют значения решения вблизи этой линии; для Х. же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Х.

Если коэффициенты уравнения (3) зависят от u , 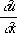и 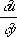(квазилинейный случай), то Х., определяемые из уравнения (4), будут разные для разных решений. Имеются определения Х. и для уравнений и систем уравнений с частными производными любого порядка.

Лит. см. при ст. Уравнения математической физики .

Характери'стикав технике, взаимосвязь между зависимыми и независимыми переменными, определяющими состояние технического объекта (процесса, прибора, устройства, машины, системы), выраженная в виде текста, таблицы, математической формулы, графика и т.п. Например, зависимости тока от электрического напряжения на участке электрической цепи (см. Вольтамперная характеристика ), расхода топлива автомобилем от пройденного им пути и состояния дороги, громкости и качества звучания громкоговорителя от частоты, времени перемагничивания ферритового сердечника от величины намагничивающего поля.

Х. по методике определения подразделяют на детерминированные (статические, динамические) и статистические; по виду аналитические зависимости — на линейные и нелинейные; по назначению — на эксплуатационные, настроечные и т.д. Статической Х. называется зависимость между выходной и входной величинами технической системы в установившихся состояниях. Динамические Х. (частотные, импульсные и др.) отражают реакции изучаемой системы на какие-либо типовые возмущающие воздействия: например, частотная Х. отражает зависимость амплитуды и фазы периодического сигнала на выходе системы от амплитуды и фазы входного гармонического сигнала при изменении только его частоты; импульсная Х. — зависимость изменения во времени сигнала на выходе системы от воздействия входного единичного импульса. В наиболее полной форме динамическая Х. содержатся в динамической математической модели объекта, например в виде дифференциальных уравнений. Статистические Х. (оценки) применяют к объектам, поведение которых во времени меняется случайным образом. К статистическим Х. относятся, например, дисперсия, автокорреляционная функция, спектральная плотность и т.п.

Линейными называются все Х., которые могут быть с заданной точностью аппроксимированы выражением вида у = ax + b , где у — выходное воздействие, x — входное воздействие изучаемой системы, а и b — постоянные коэффициенты. Все остальные Х. — нелинейные; среди них выделяют линеаризуемые Х., которые по частям с известной точностью аппроксимируются указанным выше выражением (см. Линеаризация ).

А. В. Кочеров.

Характеристи'ческая кривая,одна из важнейших характеристик фотографического материала, выражающая зависимость (при оговорённых условиях экспонирования и проявления) между оптической плотностью полученного на материале почернения фотографического и десятичным логарифмом экспозиции (называемым также количеством освещения), вызвавшей это почернение. См. ст. Сенситометрия ( рис. 1 ) и литература при ней.

Характеристи'ческая фу'нкцияв математике,

1) то же, что собственная функция .

2) Х. ф. множества А (в современной терминологии — индикатор А ) — функция f ( x ), определённая на некотором множестве Е , содержащем множество А , и принимающая значение f ( x ) = 1, если x принадлежит множеству А , и значение f ( x ) = 0, если x не принадлежит ему. 3) В теории вероятностей Х. ф. f X ( t ) случайной величины Х определяется как математическое ожидание величины e itX . Это определение для случайных величин, имеющих плотность вероятности p X ( x ), приводит к формуле

.

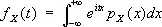Например, для случайной величины, имеющей нормальное распределение с параметрами а и s, Х. ф. равна

.

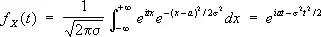Свойства Х. ф.: каждой случайной величине Х соответствует определённая Х. ф. f X ( t ); распределение вероятностей для Х однозначно определяется по f X ( t ); при сложении независимых случайных величин соответствующие Х. ф. перемножаются; при надлежащем определении понятия «близости» случайным величинам с близкими распределениями соответствуют Х. ф., мало отличающиеся друг от друга, и, обратно, близким Х. ф. соответствуют случайные величины с близкими распределениями. Указанные свойства лежат в основе применений Х. ф., в частности к выводу предельных теорем теории вероятностей. Впервые аппарат, по существу равнозначный Х. ф., был использован П. Лапласом (1812), но вся сила метода Х. ф. была показана А. М. Ляпуновым (1901), получившим с его помощью свою известную теорему.