БСЭ БСЭ - Большая Советская Энциклопедия (ЧИ)

Чиса'на(Chisana), долинный ледник на северо-восточном склоне гор Врангеля (южная Аляска) в Сев. Америке. Длина 25,8 км. Даёт начало р. Чисана — левому притоку р. Танана (бассейн р. Юкон).

Чи'сел тео'рия,наука о целых числах. Понятие целого числа , а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций.

Особое место среди целых чисел, т. е. чисел..., —3, —2, —1, 0, 1, 2, 3,..., занимают натуральные числа — целые положительные числа 1, 2, 3,...— их свойства и операции над ними. Все натуральные числа, бо'льшие единицы, распадаются на 2 класса: к 1-му классу относятся числа, имеющие ровно два натуральных делителя, именно единицу и самого себя, ко 2-му — все остальные. Числа 1-го класса стали называть простыми, а 2-го — составными. Свойства простых чисел и их связь со всеми натуральными числами изучались Евклидом (3 в. до н. э.). Если выписывать простые числа подряд, то можно заметить, что относительная плотность их убывает: на первый десяток их приходится 4, т. е. 40%, на сотню — 25, т. е. 25%, на тысячу — 168, т. е. » 17%, на миллион — 78 498, т. е. » 8%, и т.д., однако их бесконечно много (Евклид).

Среди простых чисел попадаются пары таких, разность между которыми равна двум (т. н. простые близнецы), однако конечность или бесконечность таких пар не доказана.

Евклид считал очевидным, что с помощью умножения только простых чисел можно получить все натуральные числа, причём каждое натуральное число представимо в виде произведения простых чисел единственным образом (с точностью до порядка множителей). Т. о., простые числа образуют мультипликативный базис натурального ряда. Первыми задачами о простых числах были такие: как часто они расположены в натуральном ряде и как далеко они отстоят друг от друга. Изучение распределения простых чисел привело к созданию алгоритма (правила), позволяющего получать таблицы простых чисел. Таким алгоритмом является Эратосфена решето (3 в. до н. э.). Евклид в «Началах» указал способ нахождения общего наибольшего делителя двух чисел ( Евклида алгоритм ), следствием которого является теорема об однозначном разложении натуральных чисел на простые сомножители.

Вопрос о целочисленных решениях различного вида уравнений также восходит к древности. Простейшим уравнением в целых числах является линейное уравнение аХ + bY = с , где a , b и с — попарно взаимно простые целые числа. С помощью алгоритма Евклида находится решение уравнения аХ + bY = 1, из которого затем получаются все решения первоначального уравнения. Другим уравнением в целых числах является уравнение X 2 + Y 2 = Z 2 (решение Х = 3, Y = 4, Z = 5 связано с именем Пифагора), все целочисленные решения которого выписаны в «Началах» (кн. X, предложение 29) X = r 2 —q 2, Y = 2 rq , Z = r 2 +q 2, где r и q — целые числа. Евклиду было известно также и уравнение аХ 2+1 = Y 2, названное впоследствии Пелля уравнением. В «Началах» (кн. X, предложение 9) Евклид показал, как находить все его решения, исходя из наименьшего, для случая а = 2. Систематическое изложение теории известных к тому времени уравнений в целых числах дано Диофантом в его «Арифметике» (середина 3 в. н. э.). Эта книга сыграла большую роль в дальнейшем развитии той части Ч. т., которая занимается решением уравнений в целых числах, называемых теперь диофантовыми уравнениями.

Следующий этап в развитии Ч. т. связан с именем П. Ферма , которому принадлежит ряд выдающихся открытий в теории диофантовых уравнений и в теории, связанной с делимостью целых чисел. Им была выдвинута гипотеза, получившая название Ферма великая теорема , и доказана теорема, известная как Ферма малая теорема , которая играет важную роль в теории сравнений и её позднейших обобщениях. Продолжая исследования Ферма по теории делимости чисел, Л. Эйлер доказал теорему, обобщающую малую теорему Ферма. Ему принадлежат также и первые доказательства великой теоремы Ферма для показателя n = 3.

К началу 18 в. в науке о целых числах накопилось много фактов, позволивших создать стройные теории и общие методы решения задач Ч. т.

Л. Эйлер был первым из математиков, кто стал создавать общие методы и применять др. разделы математики, в частности математический анализ, к решению задач Ч. т. Исследуя вопрос о числе решений линейных уравнений вида

a 1 X 1+... + а пХ п= N ,

где a 1,..., a n — натуральные числа, в целых неотрицательных числах X 1, ... , Xn , Л. Эйлер построил производящую функцию Ф ( z ) от переменной z , коэффициенты которой при разложении по степеням z равняются числу решений указанного уравнения. Функция Ф ( z ) определяется как формальное произведение рядов

, …,

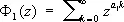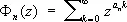
т. е. Ф ( z ) = Ф 1( z ) . ... . Ф к ( z ), каждый из которых сходится при ½ z ½ < 1 и имеет достаточно простой вид, являясь суммой членов бесконечной геометрической прогрессии:

, …,

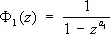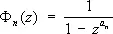
Следовательно,

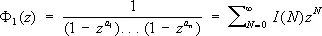
причём I ( N ) — число решений изучаемого уравнения. Метод производящих функций Эйлера послужил истоком кругового метода Харди—Литлвуда, далеко идущим развитием которого, в свою очередь, явился метод тригонометрических сумм И. М. Виноградова.

Другой проблемой Ч. т., стимулировавшей создание мощного метода, была проблема простых чисел. Л. Эйлер, доказывая теорему Евклида о бесконечности числа простых чисел, рассмотрел произведение по всем простым числам р :

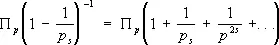
при s > 1. Это произведение сходится, и если его раскрыть, то в силу однозначности разложения натуральных чисел на простые сомножители получается, что оно равняется сумме ряда

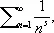
откуда следует тождество Эйлера:

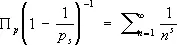, s > 1.