БСЭ БСЭ - Большая Советская Энциклопедия (ЧИ)

,

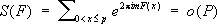при любом фиксированном ½ m ½>0, и получил нетривиальные оценки ½ S ( F )½ в случае, когда F ( x ) — многочлен, старший коэффициент которого есть иррациональное число. И. М. Виноградов, изучая распределение значений символа Лежандра на отрезках малой длины по сравнению с модулем, доказал (1914) неравенство

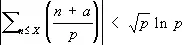, X > 0,

из которого следует, что квадратичных вычетов и невычетов на любом отрезке, длина которого чуть больше 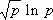, асимптотически поровну. Кроме того, он высказал гипотезу, что это будет верно при Х > р e, где e > 0 — сколь угодно малое число. В 1917 И. М. Виноградов доказал, что число целых точек в области 0 < y £ f ( x ), a < x £ b , при определённых ограничениях на порядок роста второй производной f ( x ), равно площади этой области с точностью до слагаемого порядка корня кубического из главного члена. Позднее чешским математиком В. Ярником установлено, что точность этой формулы при сделанных предположениях относительно f ( x ) нельзя существенно улучшить.

Норвежским математиком В. Бруном доказаны (1919) теоремы, которые в определённом смысле приближались к проблеме простых близнецов и проблеме Эйлера. А именно, им доказана бесконечность числа пар u 1 и u 2 , таких, что u 1— u 2= 2 и число простых делителей u 1 и u 2 не превосходит девяти; а также разрешимость уравнения u 1 + u 2= 2 N , с теми же условиями на u 1 и u 2

Г. Харди и Дж. Литлвуд опубликовали (1922—23) серию мемуаров под общим названием «Partitio Numerorum», в которых развили общий метод решения аддитивных задач Ч. т., получивший впоследствии название «кругового». Этот метод (на примере решения проблемы Варинга) состоит в следующем: пусть

[missing picture], ,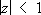

тогда

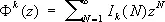
где I k ( N ) — число решений уравнений Варинга, которое находят по формуле

.

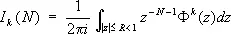Г. Харди и Дж. Литлвуд изучали последний интеграл при R ®1— 0. Окружность интегрирования определённым образом разбивается на «большие» и «малые» дуги (отчего и получил название метод), при этом интегралы по «большим» дугам дают главный член асимптотической формулы для I k ( N ), а по «малым» — остаточный. Т. о. получают асимптотическую формулу величины

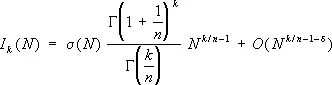
где s( N ) — некоторый «особый ряд»; s( N ) ³ с > 0, d >0 и k ³ ( n —2)2 n ¾1+ 5. С помощью этого метода Г. Харди и Дж. Литлвуд получили следующие результаты: дали новое решение проблемы Варинга, причём в форме более точной, чем это было у Д. Гильберта; дали условное решение проблемы Гольдбаха; сформулировали и выписали гипотетические формулы для количества решений большого числа уравнений с простыми числами.

В начале 30-х гг. 20 в. И. М. Виноградовым был найден т. н. метод тригонометрических сумм, позволивший решить многие проблемы Ч. т. Так, занимаясь проблемой Варинга, И. М. Виноградов обнаружил (1929), что результат Харди — Литлвуда будет значительно проще, если вместо производящих рядов рассматривать тригонометрические суммы вида

,

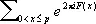где F ( x ) — действительная функция, и пользоваться соотношением

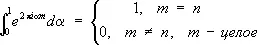
Тогда I k ( N ) в проблеме Варинга запишется так:

,

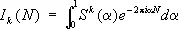где

.

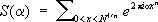Далее интервал интегрирования [0,1] разбивается рациональными несократимыми дробями вида a / b , 0 £ а < b £ t, t — параметр, зависящий от N , на подинтервалы подобные «большим» и «малым» дугам кругового метода. Интервалы, отвечающие дробям с малыми знаменателями, и сумма интегралов по ним дают главный член асимптотической формулы для I k ( N ) . Другие интервалы отвечают «малым» дугам; для них И. М. Виноградов оценивает ½ S (a)½ методом Вейля и получает остаточный член. К тригонометрическим суммам сводятся и др. задачи Ч. т.: распределение дробных долей функций, целые точки в областях на плоскости и в пространстве, порядок роста дзета-функции в критической полосе и др. Причём главным в таких задачах является вопрос о возможно более точной оценке модуля тригонометрической суммы. И. М. Виноградов предложил два метода оценок тригонометрических сумм. Первый метод (1934) дал возможность получить новые оценки сумм Вейля. Следствием этого явились современные оценки, выведена асимптотическая формула в проблеме Варинга при k ³ 4 n 2ln n , доказано, что для разрешимости уравнения Варинга при N ³ N 0 ( n ) достаточно не более 3 n ln n + 11 n слагаемых, получен новый остаточный член в асимптотических формулах для p( x ) и y( х ) (И. М. Виноградов, 1957) порядка

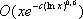, c > 0,

получено решение проблемы Гильберта — Камке (К. К. Марджанишвили , 1953).

Второй метод Виноградова (1937) позволил оценить такие тригонометрические суммы, в которых суммирование ведётся по простым числам:

.

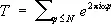Это привело к доказательству асимптотической формулы для числа представлений нечётного числа суммой трёх простых, из которой следовало, что все достаточно большие нечётные числа являются суммой трёх простых. Тем самым была решена Гольдбаха проблема. Этот метод привёл к решению других общих задач Ч. т., например проблемы Варинга в простых числах, проблемы распределения квадратичных вычетов и невычетов в последовательностях вида р + а , где р принимает значения простых чисел.

Развитие идей А. Туэ (построение вспомогательного многочлена с высокой кратностью корня) и Д. Пойа (США) (целая аналитическая функция, принимающая в целых положительных точках целые значения и растущая медленнее 2 g ½ S ½, g < 1, является многочленом) привело А. О. Гельфонда и нем. математика Т. Шнейдера (1934) к решению 7-й проблемы Гильберта, утверждающей трансцендентность чисел вида a b, a ¹0,1, b — алгебраическое число степени ³ 2. К. Зигель доказал ряд теорем о трансцендентности значений функций типа e x (т. н. Е -функции) в алгебраических точках.