БСЭ БСЭ - Большая Советская Энциклопедия (ЧИ)

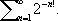
Однако вопрос об алгебраичности и трансцендентности конкретных чисел труден, и первыми были такие вопросы о классических постоянных p и е . В конце 19 — начале 20 вв. Ч. т. продолжала развиваться по многим направлениям, причём для решения отдельных задач создавались общие методы, применимые к широкому кругу задач, иногда далеко удалённых от первоначальных. Часто созданные здесь методы и понятия дают толчок развитию новых направлений.

Теория алгебраических чисел разделилась на два направления: одно изучает конкретные числа, доказывая их трансцендентность, другое изучает степень приближения алгебраических чисел рациональными или алгебраическими. В первом направлении общие методы были созданы Ш. Эрмитом (1873), доказавшим трансцендентность числа e , и немецким математиком Ф. Линдеманом (1882), доказавшим трансцендентность числа p и тем самым решившим задачу о квадратуре круга. Во втором — А. Туэ (1909) был предложен метод, с помощью которого он доказал, что в неравенстве Лиувилля к алгебраическому числу нельзя подойти существенно ближе чем Q ¾ n/ 2 . Следствием этого явилась теорема Туэ о конечности числа решений в целых числах х и у уравнения

a 0x n+ a 1x n ¾1y+... + a n ¾1xy n ¾1+ a ny n=А ,

где a 0 , a 1 , ... , a n , А — целые числа, n ³ 3.

Дальнейшее изучение простых чисел привело к новому методу в Ч. т., связанному с функцией x ( s ). Б. Риман доказал, что дзета-функция x ( s ) аналитически продолжается на всю плоскость комплексного переменного, является аналитической в каждой точке плоскости, за исключением s = 1, где она имеет полюс первого порядка с вычетом, равным 1, удовлетворяет функциональному уравнению x( s )= x(1¾ s ), где

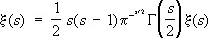
Г ( s ) — гамма-функция, и имеет бесконечно много нулей в полосе 0 £ Re s = 1 (эти нули называют нетривиальными, а полосу — критической). Он установил тесную связь между нетривиальными нулями x ( s ) и асимптотическим поведением p( х ). Изучение асимптотической формулы для функции Чебышева

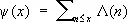
где L( n ) = ln p , если n = р к L( n ) = 0, если n ¹ p k , эквивалентно такой же задаче для функции p( х ). Функция Y( х ) может быть выражена через интеграл от производящей функции — x¢( s )/ x( s ):

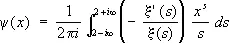
Б. Риман высказал гипотезу, что все нетривиальные нули x ( s ) лежат на прямой Re s = 1/ 2, из чего следует, что

y( x )= x + O ( 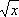ln 2 x ),

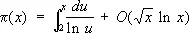
Из справедливости любой из последних формул следует гипотеза Римана. По аналогичной схеме были изучены L -ряды Дирихле. В 1896 Ш. Ла Валле Пуссен и Ж. Адамар доказали, что x( s ) ¹ 0 в области Re s ³ 1, откуда следовала формула (асимптотический закон распределения простых чисел)

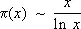
Кроме этого, Ш. Ла Валле Пуссен доказал, что x( s ) ¹ 0 в области

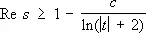
и что

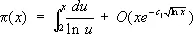
где с и c 1 — положительные постоянные. Такой же результат был получен им и для простых чисел в арифметических прогрессиях: если p( х , k , l ) — число простых чисел вида kn + 1, n £ х , k и l— взаимно простые числа, то

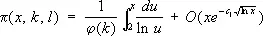
Метод получения асимптотических формул для p( х ), Y( х ), p( х , k , l ), названный методом комплексного интегрирования, нашёл многочисленные применения. Основой этого метода служит формула

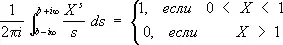
Теория квадратичных форм, начатая работами Л. Эйлера, К. Гаусса, П. Дирихле, продолжала своё развитие в работах А. Н. Коркина , Е. И. Золотарёва и А. А. Маркова. В частности, А. Н. Коркин и Е. И. Золотарёв доказали теорему: переменным любой положительной кватернарной квадратичной формы определителя D можно придать такие целые значения, что значение формы не будет превосходить величины 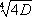, и существуют такие формы, минимумы которых равны 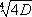. Примером такой формы является следующая:

.

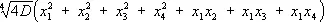Исследования А. А. Маркова относились к изучению минимумов бинарных квадратичных форм положительного определителя и привели к целому ряду новых открытий.

Проблемы целых точек в областях на плоскости получили своё дальнейшее развитие в трудах Г. Ф. Вороного , создавшего (1903) метод, с помощью которого доказано, что остаточный член в асимптотической формуле Дирихле для числа целых точек под гиперболой имеет порядок корня кубического из главного члена. Позднее (1906) метод Вороного был перенесён В. Серпиньским на проблему Гаусса целых точек в круге с тем же результатом. В это же время были предприняты попытки найти решения аддитивных проблем Ч. т. и, в частности, решить Варинга проблему. В 1909 она была решена Д. Гильбертом.

Второе, третье и четвёртое десятилетия 20 в. были исключительно богаты новыми идеями и методами в Ч. т. Г. Вейль , решая задачи, связанные с устойчивостью Солнечной системы, пришёл к понятию равномерного распределения дробных долей целочисленных функций: дробные доли действительнозначной функции F ( x ) равномерно распределены на [0,1) при х= 1,2,3.,.., если число попаданий дробных долей F ( x ) на любой интервал из [0.1) пропорционально длине этого интервала. Он доказал, что для равномерности распределения дробных долей F ( x ) необходимо и достаточно выполнение соотношения: