БСЭ БСЭ - Большая Советская Энциклопедия (ЭЙ)

Лит.: Erneström G., Verzeichnis der Schriften Leonard Eulers, Lfg 1—2, Lpz., 1910—13 (Jahresbericht der Deutschen Mathematiker—Vereinigung. Ergänzungsband 4, Lfg 1—2) [лит.]; Fuss N., Eloge de monsieur Léonard Euler..., St. Pb., 1783 (лит.); в рус. пер.— Похвальная речь покойному Леонарду Эйлеру..., в кн.: Академические сочинения, выбранные из первого тома Деяний Академии наук, под заглавием: Nova Acta Academiae scientiarum imperialis Petropolitanae, ч. 1, СПБ, 1801; Симонов Н. И., Прикладные методы анализа у Эйлера, М., 1957; Леонард Эйлер. Сб. ст., М., 1958; Рукописные материалы Л. Эйлера в Архиве Академии наук СССР, т. 1, М.—Л., 1962; Юшкевич А. П., История математики в России до 1917 года, М., 1968.

По материалам одноимённой статьи из 2-го издания БСЭ.

Л. Эйлер.

Э'йлер,Эйлер-Хельпин (von Euler-Chelpin) Ульф Сванте фон (р. 7.2.1905, Стокгольм), шведский физиолог. Сын Х. Эйлера-Хельпина. Окончил Каролинский институт в Стокгольме (1929), где с 1930 ассистент кафедры фармакологии, с 1939 профессор физиологии. В 1930 работал в лаборатории Г. Дейла в Лондоне, где открыл существование в кишечной ткани биологически активного вещества «субстанции Р». Основные труды по физиологии адренергических нервных окончаний. Установил, что норадреналин является медиатором симпатической нервной системы. Подробно исследовал его распределение в нервах и органах, обмен при разных физиологических и патологических состояниях. Обнаружил и исследовал функциональную роль простагландинов (1936) и норадреналина (1946). Открыл субклеточные частицы, содержащие норадреналин, и вскрыл механизмы захвата, хранения, освобождения норадреналина этими частицами. Член Королевской шведской АН, Датской АН, Германской академии естествоиспытателей «Леопольдина», Лондонского королевского общества (1973). Нобелевская премия (1970, совместно с Б . Кацем , и Дж . Аксельродом ).

Соч.: Noradrenaline. Springfield, 1956; Prostaglandins, N. Y.—L., 1967 (совм. с R. Eliasson).

Л. Г. Магазаник.

Э'йлера ме'тод ло'маных,один из простейших методов численного решения дифференциальных уравнений. Предложен Л. Эйлером в 1768. См. Приближённое решение дифференциальных уравнений.

Э'йлера пери'од,вычисленный Л. Эйлером на основании некоторых теоретических допущений период в движении полюсов Земли. См. Полюсы географические.

Э'йлера подстано'вки,подстановки, служащие для приведения интегралов вида

,

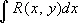где 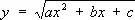и R ( x , y ) — рациональная функция от х и у , к интегралам от рациональных функций (см. Интегральное исчисление ) . Предложены Л. Эйлером в 1768. Первая Э. п.

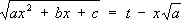
применима, если а >0; вторая Э. п.

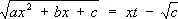
применима, если с > 0; третья Э. п.

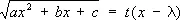
где l — один из корней трёхчлена ax 2+ bx + c , применима, если корни этого трёхчлена действительны. На практике Э. п. требуют громоздких преобразований и потому вместо них обычно пользуются теми или иными искусств. приёмами, упрощающими вычисление.

Аналогичные подстановки делаются в теории чисел при решении неопределённых уравнений 2-й степени в рациональных числах.

Э'йлера постоя'нная,предел

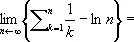С = 0,577215 ...,

рассмотренный Л. Эйлером в 1740. Эйлер дал для С ряд представлений в форме рядов и интегралов; например,

,

,

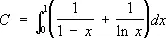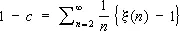где x( s ) — дзета-функция. Встречается в теории различных классов специальных функций, например гамма-функции. До сих пор неизвестно, является ли Э. п. иррациональным числом.

Э'йлера уравне'ние,

1) дифференциальное уравнение вида

, (*)

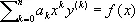где a o, ... , a n— постоянные числа; при х> 0 уравнение (*) подстановкой х = et сводится к линейному дифференциальному уравнению с постоянными коэффициентами. Изучалось Л. Эйлером с 1740. К уравнению (*) сводится подстановкой x' = ax + b уравнение

.

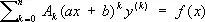2) Дифференциальное уравнение вида

,

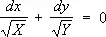где X ( x ) = a 0x 4 + a 1x 3+ a 2 x 2+ a 3x + a 4 , Y ( y ) = а 0у 4+а 1у 3 +а 2у 2 +а 3у +a 4. Л. Эйлер рассматривал это уравнение в ряде работ начиная с 1753. Он показал, что общее решение этого уравнения имеет вид F ( х , у ) = 0, где F ( х , у ) — симметричный многочлен четвёртой степени от х и у. Этот результат Эйлера послужил основой теории эллиптических интегралов.

3) Дифференциальное уравнение вида

'

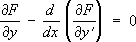служащее в вариационном исчислении для разыскания экстремалей интеграла

.

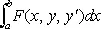Выведено Л. Эйлером в 1744.

Э'йлера уравне'ния,

1) в механике — динамические и кинематические уравнения, используемые при изучении движения твёрдого тела; даны Л. Эйлером в 1765.

Динамические Э. у. представляют собой дифференциальные уравнения движения твёрдого тела вокруг неподвижной точки и имеют вид

I x 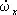+ ( I z— I y) w yw z = M x ,

I y 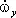+ ( I x— I z ) w z w x= M y, (1)

I z 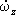+ ( I y — I x ) w x w y = M z ,