БСЭ БСЭ - Большая Советская Энциклопедия (ЭЙ)

где I x , I y, I z— моменты инерции тела относительно гл. осей инерции, проведённых из неподвижной точки, w х , w у, w z— проекции мгновенной угловой скорости тела на эти оси, M x , M y, M z— гл. моменты сил, действующих на тело, относительно тех же осей; 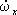, , 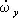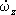— проекции углового ускорения.

Кинематические Э. у. дают выражения w х , w у, w z через Эйлеровы углы j, y, q и имеют вид

w x = 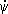sin q sin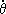j + cosj,

w у= 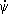sin q cosj — 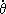sinj, (2)

w z = 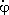+ 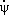cos q.

Система уравнений (1) и (2) позволяет, зная закон движения тела, определить момент действующих на него сил, и, наоборот, зная действующие на тело силы, определить закон его движения.

2) В гидромеханике — дифференциальные уравнения движения идеальной жидкости в переменных Эйлера. Если давление р , плотность r, проекции скоростей частиц жидкости u , u , w и проекции действующей объёмной силы X , У , Z рассматривать как функции координат x , у , z точек пространства и времени t (переменные Эйлера), то Э. у. в проекциях на прямоугольные декартовы оси координат будут:

,

,

.

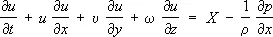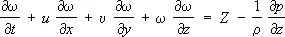Решение общей задачи гидромеханики в переменных Эйлера сводится к тому, чтобы, зная X , У , Z , а также начальные и граничные условия, определить u , u, w, р , r, как функции х , у , z и t. Для этого к Э. у. присоединяют уравнение неразрывности в переменных Эйлера

.

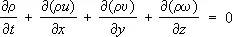В случае баротропной жидкости, у которой плотность зависит только от давления, 5-м уравнением будет уравнение состояния r = j ( р ) (или r — const, когда жидкость несжимаема).

Э. у. пользуются при решении разнообразных задач гидромеханики.

Лит.: Бухгольц Н. Н., Основной курс теоретической механики, ч. 2, 9 изд., М., 1972, §14, 16; Лойцянский Л. Г., Механика жидкости и газа, 4 изд., М., 1973.

С. М. Тарг.

Э'йлера фо'рмулыв математике, важнейшие формулы, установленные Л. Эйлером.

1) Э. ф., связывающие тригонометрические функции с показательной (1743):

e ix = cos х + i sin х ,

, .

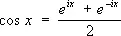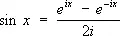2) Э. ф., дающая разложение функции sin х в бесконечное произведение (1740):

.

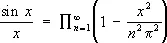3) Тождество Эйлера о простых числах:

,

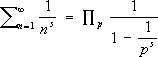где s = 1, 2,..., и произведение берётся по всем простым числам р.

4) Тождество Эйлера о четырёх квадратах:

( a 2+ b 2 + c 2 + d 2)( p 2 + q 2 + r 2 + s 2 = x 2 +y 2 +z 2 +t 2, где

,

,

,

.

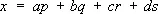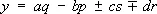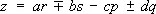5) формула Эйлера о кривизнах (1760):

.

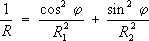Она даёт выражение кривизны 1 /R любого нормального сечения поверхности через её главные кривизны 1 /R 1и 1/ R 2и угол j между одним из главных направлений и данным направлением.

Эйлеру принадлежит также Эйлера—Маклорена формула суммирования, Эйлера—Фурье формулы для коэффициентов разложений функций в тригонометрические ряды.

Лит. см. при ст. Эйлер.

Э'йлера фу'нкция,число j( а ) натуральных чисел, меньших, чем а , и взаимно простых с а :

,

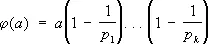где p 1 , ... , p k— простые делители числа а. Введена Л. Эйлером в 1760—61. Если числа а и b взаимно просты, тоj( ab ) = j( а ) j( b ). При т> 1 и наибольшем общем делителе ( а , m ) = 1, а , m — взаимно просты, имеет место сравнениеa j( m ) = 1 (mod m ) (теорема Эйлера). Э. ф. встречаются во многих вопросах чисел теории .

Э'йлера чи'слав математике, целые числа Е п , являющиеся коэффициентами при t n/ n !, в разложении функции 1 / ch t (см. Гиперболические функции ) в степенной ряд:

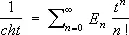
Введены Л. Эйлером в 1755. Э. ч. связаны рекуррентным соотношением ( Е +1) n+( E ¾1) n= 0, n = 1, 2, 3,..., E 0= 1 (после возведения в степень надо вместо E k подставить E k ) и с Бернулли числами — соотношениям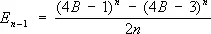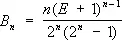и

,

и .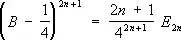

Встречаются в различных формулах математического анализа.

Э'йлера число',один из подобия критериев движения жидкостей или газов. Характеризует соотношение между силами давления, действующими на элементарный объём жидкости или газа, и инерционными силами. Э. ч. Eu определяют формулой