Альфред Фрост - Волновой принцип Эллиотта: Ключ к пониманию рынка

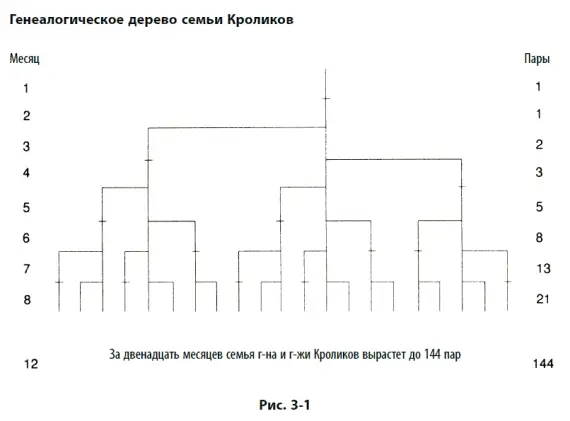
Сумма любых двух соседних чисел последовательности равна следующему за ними члену: так, 1 плюс 1 равно 2, 1 плюс 2 равно 3, 2 плюс 3 равно 5, 3 плюс 5 равно 8 и так далее до бесконечности.

После нескольких первых чисел последовательности отношение любого ее члена к последующему приблизительно равно 0,618, а к предшествующему – 1,618. Чем больше порядковый номер члена последовательности, тем ближе отношение к числу фи (обозначается φ), являющемуся иррациональным числом и равному 0,618034… Отношение между членами последовательности, разделенными одним числом, примерно равно 0,382, а обратное ему число равно 2,618. На рис. 3–2 приведена таблица соотношений всех чисел Фибоначчи от 1 до 144.

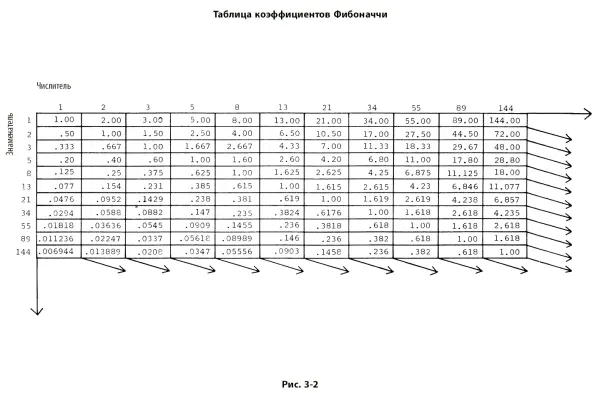
φ является единственным числом, которое, будучи прибавленным к 1, дает обратное себе число: 1 + 0,618 = 1: 0,618. Это родство процедур сложения и умножения приводит к следующей последовательности уравнений:

0,6182 = 1–0,618

0,6183 = 0,618 – 0,6182

0,6184 = 0,6182 – 0,6183

0,6185 = 0,6183 – 0,6184

или

1,6182 = 1 + 0,618

1,6183 = 1,618 + 0,6182

1,6184 = 1,6182 + 0,6183

1,6185 = 1,6183 + 0,6184

Некоторые взаимосвязанные свойства этих четырех основных коэффициентов перечислены ниже:

1,618 – 0,618 = 1

1,618 × 0,618= 1

1 – 0,618 = 0,382

0,618 × 0,618 = 0,382

2,618 – 1,618 = 1

2,618 × 0,382= 1

2,618 × 0,618= 1,618

1,618 × 1,618 = 2,618

Если любое число Фибоначчи, кроме 1 и 2, умножить на четыре и прибавить к определенному числу Фибоначчи, то получится другое число Фибоначчи, так что:

3 × 4 = 12; + 1 = 13

5 × 4 = 20; + 1 = 21

8 × 4 = 32; + 2 = 34

13 × 4 = 52; + 3 = 55

21 × 4 = 84; + 5 = 89

и т. д.

По мере роста новой прогрессии числа образуют третью последовательность, составленную из чисел, прибавленных к произведению четверки и числа Фибоначчи. Это делается возможным в связи с тем, что отношение между членами последовательности, отстоящими друг от друга на две позиции, равно 4,236, где число 0,236 является обратным к 4,236 и, кроме того, разностью между 4,236 и 4. Другие множители приводят к другим последовательностям, все они основаны на коэффициентах Фибоначчи.

Мы предлагаем вашему вниманию список некоторых дополнительных свойств, связанных с последовательностью Фибоначчи:

1. Никакие из двух последовательных чисел Фибоначчи не имеют общих делителей.

2. Если члены последовательности Фибоначчи пронумеровать как 1, 2, 3, 4, 5, 6, 7 и т. д., мы обнаружим, что, за исключением четвертого члена (число 3), номер любого числа Фибоначчи, являющегося простым числом (т. е. не имеющим иных делителей, кроме себя самого и единицы), также простое число. Сходным образом, за исключением четвертого члена последовательности Фибоначчи (число 3), все составные номера членов последовательности (т. е. те, что имеют как минимум два делителя за исключением себя самого и единицы), соответствуют составным числам Фибоначчи, что и показывает приведенная ниже таблица. Обратное не всегда оказывается верным.

3. Сумма любых десяти членов последовательности делится на одиннадцать.

4. Сумма всех чисел Фибоначчи до определенной точки последовательности плюс единица равна числу Фибоначчи, отстоящему на две позиции от последнего прибавленного числа.

5. Сумма квадратов любых последовательных членов, начинающихся с первой 1, всегда будет равна последнему (из данной выборки) числу последовательности, умноженному на следующий член.

6. Квадрат числа Фибоначчи минус квадрат второго члена последовательности в сторону уменьшения всегда будет числом Фибоначчи.

7. Квадрат любого числа Фибоначчи равен предыдущему члену последовательности, умноженному на следующее число в последовательности, плюс или минус единица. Прибавление и вычитание единицы чередуются по мере развития последовательности.

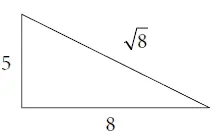
8. Сумма квадрата числа Fn и квадрата следующего числа Фибоначчи Fn + 1 равна числу Фибоначчи F2n + 1. Формула Fn2 + Fn + 12 = F2n + 1 применима к прямоугольным треугольникам, где сумма квадратов двух более коротких сторон равна квадрату самой длинной стороны. Справа приведен пример, использующий F5, F6 и квадратный корень из F11.

9. Формула, показывающая отношение между двумя наиболее распространенными иррациональными числами в математике π и φ:

Fn= 100 × π2 × φ(15 – n), где φ = 0,618…, n представляет собой порядковый номер в последовательности и Fn представляет сам по себе член последовательности. В данном случае число 1 представлено только один раз, так что F1 ≈ 1, F2 ≈ 2, F3 ≈ 3, F4 ≈ 5 и т. д.

Например, пусть n = 7. Тогда

F7 ≈ 100 × 3,14162 × 0,6180339(15 – 7) ≈

≈ 986,97 × 61803368 ≈

≈ 986,97 × 0,021129 ≈ 21,01 ≈ 21.

10. Одно из удивительных явлений, которое, насколько нам известно, до сих пор не упоминалось, состоит в том, что отношения между числами Фибоначчи равны числам, очень близким к тысячным долям других чисел Фибоначчи, при разности, равной тысячной доле еще одного числа Фибоначчи (см. рис. 3–2). Так, в направлении возрастания отношение двух идентичных чисел Фибоначчи равно 1, или 0,987 плюс 0,013; соседние числа Фибоначчи имеют отношение 1,618, или 1,597 плюс 0,021; числа Фибоначчи, расположенные с двух сторон от некоторого члена последовательности, имеют отношение 2,618, или 2,584 плюс 0,034, и т. д. В обратном направлении соседние числа Фибоначчи имеют отношение 0,618, или 0,610 плюс 0,008; числа Фибоначчи, расположенные с двух сторон от некоторого члена последовательности, имеют отношение 0,382, или 0,377 плюс 0,005; числа Фибоначчи, между которыми расположены два члена последовательности, имеют отношение 0,236, или 0,233 плюс 0,003; числа Фибоначчи, между которыми расположены три члена последовательности, имеют отношение 0,146, или 0,144 плюс 0,002; числа Фибоначчи, между которыми расположены четыре члена последовательности, имеют отношение 0,090, или 0,089 плюс 0,001; числа Фибоначчи, между которыми расположены пять членов последовательности, имеют отношение 0,056, или 0,055 плюс 0,001; числа Фибоначчи, между которыми расположено от шести до двенадцати членов последовательности, имеют отношения, которые сами являются тысячными долями чисел Фибоначчи, начиная с 0,034. Интересно, что в этом анализе коэффициент, связывающий числа Фибоначчи, между которыми располагаются тринадцать членов последовательности, снова начинает ряд с числа 0,001, с тысячной доли того числа, где он начался! При всех подсчетах мы действительно получаем подобие или «самовоспроизведение в бесконечном ряду», раскрывающее свойства «самой прочной связи среди всех математических отношений».