Альфред Фрост - Волновой принцип Эллиотта: Ключ к пониманию рынка

Как и в случае золотого сечения, значение золотого прямоугольника не исчерпывается его красотой, но, по-видимому, обслуживает и функциональные задачи. Среди множества примеров наиболее удивительный состоит в том, что двойная спираль ДНК сама создает точные золотые прямоугольники, изгибаясь с правильными интервалами (см. рис. 3–9).

В то время как золотое сечение и золотой прямоугольник представляют собой статичные формы природной или рукотворной красоты и функциональности, наиболее ярким представлением эстетически приятного динамизма, упорядоченного роста или прогресса является одна из наиболее замечательных форм во Вселенной – золотая спираль.

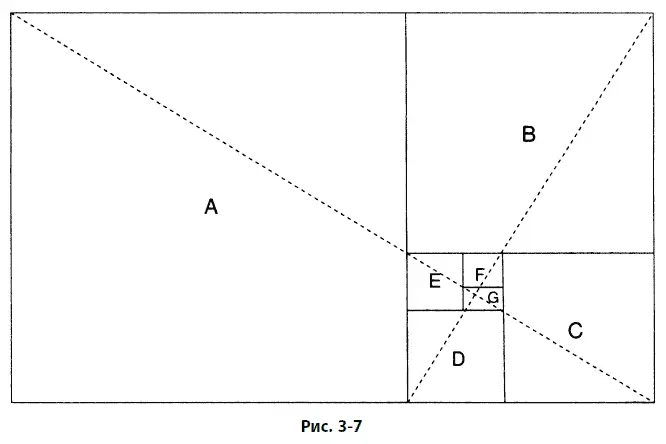
Для построения золотой спирали может быть использован золотой прямоугольник. Каждый золотой прямоугольник может быть поделен на квадрат и меньший золотой прямоугольник, как показано на рис. 3–6. Процесс такого деления теоретически может продолжаться бесконечно. Нарисованные в результате квадраты закручиваются внутрь, мы их пометили как A, B, C, D, E, F и С

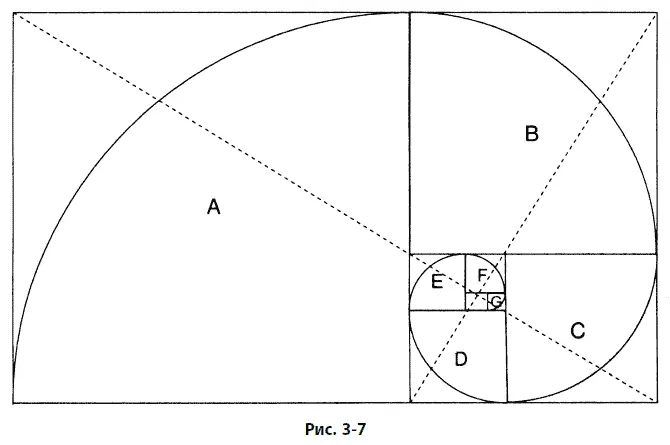
Пунктирные отрезки, которые сами имеют золотое отношение друг к другу, делят прямоугольник по диагоналям и указывают теоретический центр закручивающихся квадратов. Начав рядом с этой точкой, мы можем нарисовать спираль, показанную на рис. 3–7, соединив кривой точки пересечения закручивающихся квадратов в направлении их увеличения. По мере того как квадраты закручиваются внутрь и наружу, точки их соединения указывают путь золотой спирали.

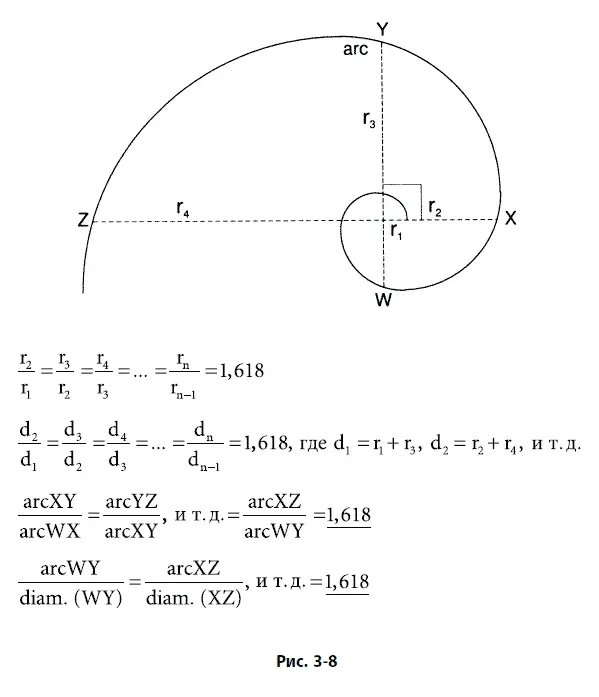
В любой точке золотой спирали отношение длины дуги к ее диаметру равно 1,618. Отношение диаметров и радиусов, отстоящих друг от друга на 90°, в свою очередь, равно 1,618, что и показано на рис. 3–8.

Золотая спираль, являющаяся логарифмической, или равноугольной, спиралью, не имеет границ и обладает постоянной формой. Из любой своей точки спираль может быть бесконечно продолжена как внутрь, так и наружу. Центр никогда не достигается, и наружу спираль простирается бесконечно. Ядро логарифмической спирали на рис. 3–8, если посмотреть на него под микроскопом, имело бы тот же вид, что и ее продолжение, если на него посмотреть с расстояния световых лет.

Если фигуры Евклидовой геометрии (может быть, за исключением эллипса) в типичном случае подразумевают статичность, спираль содержит движение: рост и уменьшение, развертывание и сжатие, прогресс и регресс. Логарифмическая спираль оказывается сущностным выражением явления естественного роста, обнаруживаемого во Вселенной повсеместно. Ее придерживаются и такие мелкие движения, как движение атомарных частиц, и такие огромные, как движение галактик. Как указывал Дэвид Бергамини в своей «Математике», написанной для серии «Time-Life Books’ Science Library», хвост кометы изгибается по направлению от Солнца по логарифмической спирали. Бактерии растут с ускорением, график которого имеет вид логарифмической спирали. Электронный микроскоп, наведенный на искусственный кристалл, обнаруживает логарифмические спирали. Еловые шишки, морские коньки, раковины моллюсков и улиток, океанские волны, папоротник, рога животных и расположение семечек подсолнуха или маргаритки – все это образует логарифмические спирали. Ураганы, водовороты и галактики внешнего космоса закручиваются в логарифмические спирали. Даже человеческий палец, составленный из трех костей, образующих по отношению друг к другу золотое сечение, принимает спиральную форму в согнутом виде. На рис. 3–9 мы видим отражение этого космического влияния во множестве форм. Миллионы лет и световые годы разделяют еловую шишку и спираль Млечного Пути, но устройство их одинаково: коэффициент 1,618, вероятно, есть первичный закон, управляющий динамикой природных явлений. Золотая спираль разворачивается перед нами как символ одного из величайших замыслов природы, как сила нескончаемого расширения и сжатия, статичный закон, управляющий динамическими процессами и основанный на коэффициенте 1,618 – отношении золотой середины.

На протяжении веков величайшие умы мира по достоинству оценивали значение этого вездесущего явления. История изобилует примерами ученейших людей, очарованных этой математической формулой. Пифагор в качестве символа Порядка выбрал пятиконечную звезду, в которой каждый отрезок находится в золотом отношении к следующему отрезку; знаменитый математик XVII в. Якоб Бернулли приказал, чтобы золотая спираль была выбита на его надгробии; Исаак Ньютон спал на кровати (сегодня она принадлежит фонду Gravity Foundation в Новом Бостоне), на изголовье которой была вырезана все та же золотая спираль. Первыми из известных приверженцев золотого отношения были строители пирамиды в Гизе, зафиксировавшие свое знание числа φ в ее конструкции почти 5000 лет назад. Египетские инженеры сознательно использовали золотое отношение в Великой Пирамиде, придав ее лицевым сторонам наклонную высоту, равную половине длины ее основания, умноженной на 1,618. Таким образом, вертикальная высота пирамиды равна квадратному корню из произведения половины ее основания на 1,618. По словам Питера Томпкинса, автора книги «Секреты Великой Пирамиды» (Harper & Row, 1971), «это отношение действительно показывает справедливость слов Геродота о том, что квадрат высоты пирамиды равен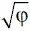

×

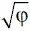
= φ, а площади ее фасадов 1 × φ = φ». Более того, применяя такие пропорции, математически искушенные египтяне (очевидно для того чтобы построить масштабированную модель Северного полушария) использовали числа π и φ в своих попытках нахождения квадратуры круга и кубатуры сферы (т. е. в попытках построить круг, равный по площади квадрату, и куб, равный по объему сфере). Увы, и спустя четыре тысячи лет эти задачи не были решены.

Несмотря на то что простое упоминание Великой Пирамиды может служить основанием для скептицизма (возможно, оправданного), не забывайте о том, что ее форма отражает те же чары, под обаянием которых находились столпы научной, математической, художественной и философской мысли, и среди них Платон, Пифагор, Бернулли, Кеплер, да Винчи и Ньютон. Строители пирамиды тоже были, несомненно, великолепными учеными, астрономами, математиками и инженерами. Они хотели сохранить золотое отношение на тысячелетия как нечто исключительно важное. То, что интеллектуалы такого калибра взяли на себя эту задачу (а к ним позже присоединились некоторые величайшие умы Древней Греции и эпохи Просвещения), само по себе поучительно. Что же касается причины, все, что у нас есть, – это предположения многочисленных авторов. Такие предположения, какими бы абсурдными они ни казались, имеют прямое отношение к нашим собственным наблюдениям. Высказывались догадки, что на протяжении веков после завершения ее строительства Великая Пирамида использовалась как храм, в котором получали посвящение те, кто доказали свое право на приобщение к великим тайнам мироздания. Лишь тот, кто мог подняться над незрелостью принятия вещей такими, какими они кажутся, и открыть, чем они на самом деле являются, мог участвовать в так называемых «мистериях», где раскрывались сложные «тайны» вечного истинного порядка.