Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 …

Что останется, если мы сбросим каждую вторую карту, начиная с первой? Только четные позиции, а это означает, что 16-я карта останется на месте:

2 4 6 8 10 12 14 16 18 …

Мы снова сбрасываем каждую вторую карту, и остаются следующие позиции:

4 8 12 16 …

а потом

8 16

и, наконец,

16.

Эта модель показывает, что как при большем, так и при меньшем числе карт происходит одно и то же. Очевидно, что 16-я карта остается в любом случае, если убирать каждую вторую.

Однако у нас остается проблема, связанная с «…». Здесь мы наблюдаем важное свойство абстрагирования.Если отбросить важную деталь, то мы, вероятно, получим неправильный ответ. Логическое мышлениетоже с легкостью заведет вас не туда, если не продумать в точности все возможные варианты. Если бы в начале фокуса мы разделили колоду в какой-то точке до 16-й карты, то, конечно, эта карта ушла бы при первом разделении. Тогда у нас осталась бы другая карта, например восьмая. Возможно, вы поняли это, как только обратились к абстрагированию. Однако есть еще одна похожая, но немного более тонкая проблема. Давайте снова проведем моделирование, но увеличим масштаб. Результат показан на рис. 7.

Ну и ну. Если взять 32 карты или больше, у нас останется не 16-я карта, а 32-я. Таким образом, даже если мы добьемся того, что 16-я карта не будет сброшена в начале, фокус не сработает, если не подготовиться заранее. Нам нужно добавить еще одно условие. Как показали логические рассуждения, колоду необходимо разделить в каком-то месте после 16-й и перед 32-й картой. Поэтому важно сказать добровольцу, что нужно отбросить «примерно половину». Однако на самом деле подразу­мевается не примерное разделение, а весьма точное — «между 16-й и 32-й картой». Вот почему нужно ограничить руками пространство над 16-й и 32-й картами, чтобы сориентировать добровольца при делении колоды. Это делается для того, чтобы условие, или, как выразился бы программист, входное условие,было выполнено без ведома добровольца.

Итак, мы использовали численное моделированиеи логическое мышлениеи таким образом убедились, что фокус действительно работает, но при условии, что перед тем, как мы начинаем сбрасывать карты, их в колоде минимум 16 и максимум 31. Численное моделирование — это создание моделей вычислительных процессов с целью их изучения. Здесь мы прибегли к моделированию, чтобы посмотреть, всегда ли получается фокус, но подобным образом можно провести и обобщение. Наша модель показывает принцип, лежащий в основе фокуса. Главное в нем — не игральные карты. Мы абстрагировались от них, как и от многих других деталей. Выявив этот базовый принцип, мы можем придумать другие варианты фокуса, основанные на нем. Мы еще вернемся к этому позже.

Наш фокус имеет с вычислительными алгоритмами связь более глубокую, чем то, что и фокус, и программы являются алгоритмами. Вариант алгоритма фокуса применялся в ранних компьютерах для поиска по данным, записанным на перфокарты. Перфокарты — это физически существующие карты, которые использовали в качестве долгосрочной памяти, чтобы хранить данные для последующей обработки.

Информацию записывали на перфокарты, пробивая в них отверстия в соответствии с кодом, немного похожим на шпионский шифр. В то время как у шпионов бывают в ходу таинственные символы, для компьютеров применялся код из отверстий и их отсутствия. В отличие от шпионского кода, в компьютерном коде значения символов должны быть известны всем заинтересованным лицам. Специальный код, который до сих пор используют в компьютерах для простых чисел, называется двоичным.

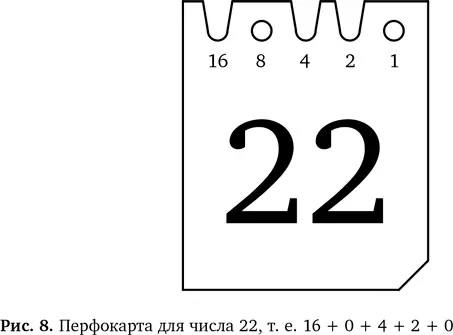
На рис. 8 приведен пример перфокарты для числа 22. Чтобы увидеть, как использовать перфокарты для поиска данных с помощью магического принципа «шиворот-навыворот», давайте сделаем их сами, а потом посмотрим, как они действуют.

Шаблоны для перфокарт можно скачать здесь: www.cs4fn.org/punchcards/.

Распечатайте их — в идеале прямо на тонком картоне — и слегка посыпьте тальком, чтобы они не склеивались (это важно).

Вместо отверстий и их отсутствия мы будем использовать в нашем коде отверстия и небольшие вырезы. Вам следует сделать вырезы в нужных местах, чтобы в сумме получилось число, крупно написанное на карте. Например, на карте 22 есть вырезы напротив 16, 4 и 2, а 16 + 4 + 2 = 22. Чтобы понять происходящее, нужно знать кое-что из простой математики, а именно двоичную систему счисления.

Двоичный код — это способ записывать числа, при котором в нашем распоряжении 0 и 1 вместо 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которыми мы обычно пользуемся. Наша обычная система называется десятичной. В двоичной системе всего два символа, и на перфокартах мы будем использовать круглые отверстия для 0 и щели для 1. Двоичная и десятичная системы — просто две разные системы представления чисел. Выбрать правильное представлениеинформации — еще один важный элемент вычислительного мышления.

Давайте сначала рассмотрим десятичную систему и сравним ее с двоичной. В десятичной системе, чтобы досчитать до 9, мы используем цифры, но они заканчиваются, и в этот момент мы переходим в новый столбик. Мы возвращаемся к 0, но переносим 1 в следующий столбик, и 1 теперь обозначает 10, как показано на рис. 9.

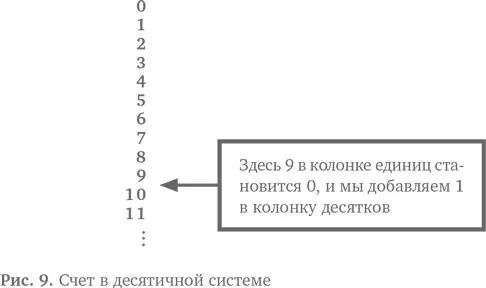
Любая цифра во втором столбике обозначает на 10 больше, чем та же цифра в первом столбике. В десятичной системе 16 — это один десяток (1 в столбике десятков) и шесть единиц (6 в столбике единиц). Мы добавляем 10 к 6, чтобы получить число 16. Подобным образом, 987 обозначает 9 раз по 100, 8 раз по 10 и 7 раз по одному, сложенные вместе.

Двоичная система работает точно так же, только у нас раньше заканчиваются цифры. Дойдя до 1, мы уже переходим в новый столбик, до 9 нам не добраться (рис. 10). Это значит, что столбцы теперь предназначены для единиц, двоек, четверок, восьмерок и так далее — вместо единиц, десятков и сотен. То есть в двоичной системе (используя только 1 и 0) мы записываем, например, число 5 как 101. Это 1 в разряде четверок плюс 0 в разряде двоек и плюс 1 в разряде единиц.

Если распределить это на пять колонок (как мы сделаем это на перфокартах), то 5 в двоичной системе будет выглядеть как 00101.

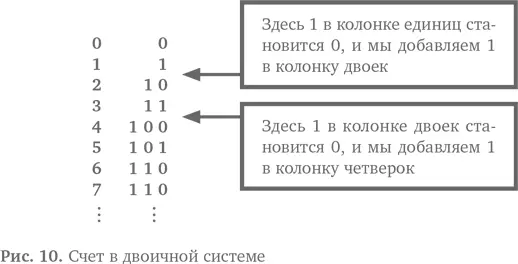
Подобным образом, 16 в двоичной системе — это 10000.