Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

Вычислительное мышление подразумевает умение мыслить логически. Хорошее представление информации помогает в этом, потому что позволяет убрать ненужное и сосредоточиться на главном. Именно это и обнаружил Леонард Эйлер, когда решал задачу «Мосты Кенигсберга» и пришел к мысли нарисовать граф (рис. 39). Граф помог ему увидеть задачу предельно ясно.

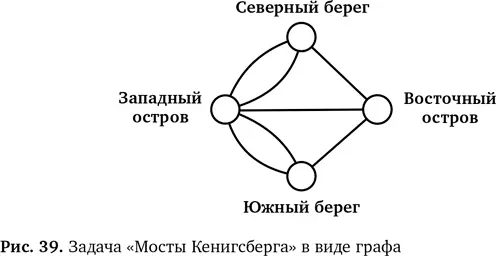
Глядя на граф, Эйлер осознал, что найти ответ невозможно. Почему? Подходящий маршрут должен затронуть все вершины и обойти все ребра, но только один раз (поскольку ребра — это мосты, а нам сказали, что по каждому мосту можно пройти один раз). Давайте предположим, что такой маршрут существует, и, чтобы его показать, нарисуем пунктирные линии со стрелками вдоль ребер. Все ребра должны входить в маршрут, а значит, все они должны совпасть с пунктирными стрелками. Возьмем вершину на этом маршруте, как показано на рис. 40. На каждую пунктирную стрелку, направленную от нее, должна приходиться пунктирная стрелка, направленная к ней. В противном случае маршрут зайдет в тупик — когда пойдет по лишнему ребру, над которым не будет пунктирной стрелки. Из этого тупика не получится выйти без возвращения на уже пересеченный мост. То же относится и к любой вершине. Поэтому, чтобы искомый маршрут был возможен, у всех вершин должно быть четное число связанных с ними ребер.

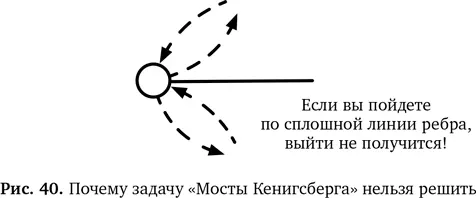
Все вершины на графе Кенигсберга имеют нечетное число ребер, поэтому искомый маршрут невозможен. Однако со времен Эйлера через реку построили новый мост, поэтому граф изменился. Экскурсоводам современного Калининграда живется легче.

Мы рассмотрели простые головоломки с поиском маршрута. Теперь возьмем задачу из реальной жизни. Представьте, что специалист по продажам каждый день настраивает навигатор, чтобы найти самый короткий путь, позволяющий по одному разу посетить несколько клиентов в разных городах и снова оказаться в офисе, не возвращаясь по собственным следам.

Такую кратчайшую дорогу можно просчитать, но вряд ли получится каждый раз делать это за разумный промежуток времени. Даже если надо побывать у 20 клиентов, нельзя гарантировать, что вы ежедневно будете находить оптимальное решение — на это потребуется слишком много времени. И дело не в том, что требуется более мощный навигатор или компьютер. Если число мест, где необходимо побывать, достаточно велико (на самом деле оно не очень-то и велико), то на поиск совершенного решения уйдет больше времени, чем прошло с момента возникновения Вселенной, — даже при наличии самого быстрого компьютера! Почему? Потому что число возможных вариантов, которые необходимо проверить, стремительно растет с появлением каждого нового города. Даже если навигатор запрограммировать на какое-то решение, нельзя гарантировать, что оно будет безупречным. Заложенный в программу способ не обеспечит кратчайшего пути. Вполне вероятно, что в программе сработает так называемый жадный алгоритм.Давайте изменим условия задачи, чтобы понять, о чем идет речь.

Представьте, что вы отправляетесь в долгий отпуск, мечтая хорошо отдохнуть. Открытый чемодан лежит на кровати. Вы уже упаковали одежду и теперь собираете вещи, которые хотите взять с собой, — книги, настольные игры, пазлы, колоду карт, краски и бумагу… Все, что, по вашему мнению, поможет расслабиться. Все эти вещи разного размера. Их нужно сложить в чемодан. Как это сделать? Пробуем разные варианты. Сначала пазл, потом игральные карты, потом книга с кроссвордами — и так далее. Если у вас достаточно места, то все получится, однако, если места маловато или вы не хотите брать много чемоданов, намечается проблема.

Хорошей альтернативой будет жадный алгоритм. С его помощью не получится упаковать все максимально компактно, но порой он работает весьма хорошо. Как выбрать, что положить сначала? Исходите из жадности. Положите самый большой предмет внутрь, пусть он займет как можно больше места. Теперь положите следующий по размеру — и так далее. Если что-то не помещается, берите следующий чемодан. Обычно все получается само собой, потому что, когда у вас остаются небольшие свободные пространства, вы заполняете их небольшими предметами. Это годный эвристическийалгоритм — с такими алгоритмами вы достаточно хорошо (но не безупречно) справитесь с задачей. Они не гарантируют оптимального решения.

Основная идея жадного алгоритма применима и при разработке маршрута для коммивояжера. Используя ту же идею обобщения, вы на каждом этапе выбираете ближайший к точке отправления город. При этом не всегда получается оптимальный вариант, но можно рассчитывать на хороший результат за разумное время.

Идея прокладывания маршрута между точками, которая при подходящем обобщениидает граф, возникает снова и снова при решении самых разных задач. Как только вы осознали, что это граф, в вашем распоряжении сразу оказывается много алгоритмов. Тогда некоторые задачи оказываются легкими, а другие — нерешаемыми. Однако интереснее всего те, что по мере роста масштаба задачи утрачивают рациональность решения. В этом случае необходимо правильно податьинформацию и выбрать алгоритм. К примеру, важно вовремя заметить, что проблема становится сложной и лучше использовать эвристический алгоритм.

Выбор подачи информации и алгоритма может быть хорошим или плохим. Некоторые варианты подачи и алгоритмов просто красивы — их элегантность доставляет настоящее удовольствие в процессе решения задачи.

Теперь, ознакомившись с основами вычислительного мышления, рассмотрим, как с его помощью создать искусственный разум для робота. Строить тело робота интересно, но без «мозга» оно ни на что не способно. Мы изучим историю роботостроения, выясним, что такое «понимать», и создадим систему искусственного интеллекта — виртуального собеседника, или чат-бота.

Термин «робот» впервые появился в пьесе R.U.R. («Россумские универсальные роботы») чешского писателя-публициста Карела Чапека. В этой пьесе на заводе, расположенном на уединенном острове, делают человекоподобных роботов, «труд которых в пять раз дешевле человеческого». По ходу действия разворачивается знакомый сюжет, который заканчивается тем, что (подумать только!) все люди, за исключением одного, погибают во время восстания роботов. В финале последний человек совершает акт самопожертвования и заставляет двух роботов полюбить друг друга. Занавес.