Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

Чтобы написать алгоритм, который позволит компьютеру определить края, необходимо хорошее представление.Изображение легко представить в виде набора чисел, используя разные значения для светло-серого и темно-серого. Благодаря этому мы используем математику в алгоритмах обработки. Условимся, что светло-серый — это число 3, а темно-серый — 4. Например, эти числа могли бы показывать количество чернил, необходимое для печати пиксела. Изображение только из чисел показано на рис. 64 b.

Граница никуда не делась, но нам, людям, теперь гораздо сложнее ее увидеть. Она существует только в виде численной закономерности, а мы от природы не обладаем способностью обрабатывать такие закономерности так же хорошо, как изображения. Но, как мы увидим далее, представлениеоблегчит этот процесс для машины.

Теперь давайте посмотрим на еще более мелкий и скучный образец, представленный на рис. 65. Он состоит всего лишь из трех пикселов, однако, надо признать, в нем есть отрицательное число, что делает его немного более интересным. Но как это поможет компьютеру видеть нечто простое? В информатике такой шаблон называется цифровым фильтром.Как и любой фильтр, например в кофеварке, он пропускает лишь нечто определенное. В данном случае — определенные наборы чисел вместо кофе.

Чтобы цифровой фильтр заработал, его накладывают на исходный набор чисел, и элемент за элементом по шаблону умножается на коэффициент. Результаты по всем элементам суммируются, и на выходе получается окончательное значение.

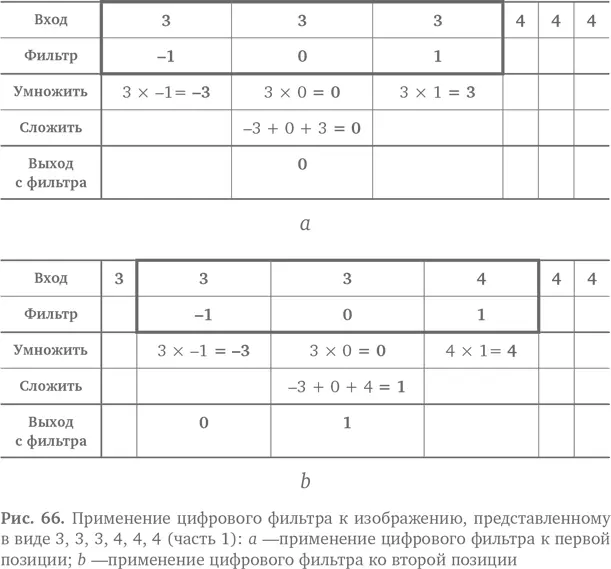
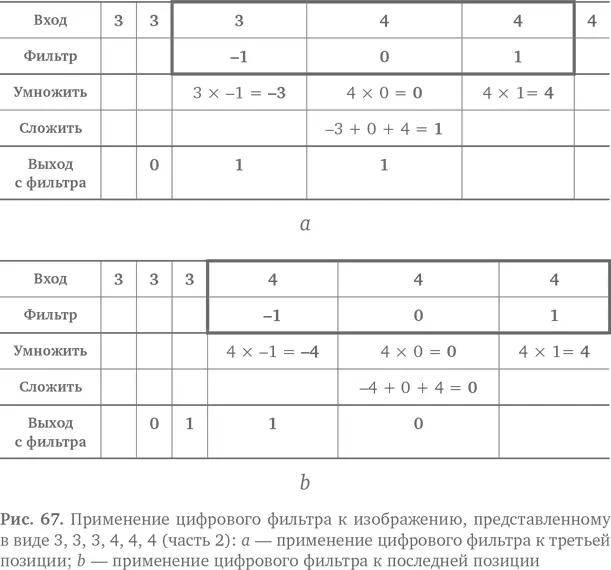
Рассмотрим пример. Допустим, входной набор чисел, представляющий изображение, — 3, 3, 3, 4, 4, 4. Мы применяем к нему фильтр. Как это будет выглядеть для первых трех чисел, показано на рис. 66 а. Мы умножаем фильтр на соответствующие числа, получаем −3, 0 и 3, потом складываем их и получаем 0. Это новое значение на выходе фильтра. Теперь фильтр перемещается, словно на конвейере, на один элемент. Он накладывается на новые входные цифры и дает следующий результат на выходе, как показано на рис. 66 b. Пожалуйста, двигайтесь дальше! Фильтр сдвигается еще на один шаг, нависает над новыми числами и дает следующий результат. Получается как на рис. 67 a. Наконец, передвинувшись еще на один шаг вправо, наш трудолюбивый фильтр доходит до конца, и на выходе появляется последний результат, как на рис. 67 b.

И где мы оказались после всех этих математических операций? Давайте посмотрим, что у нас есть, не обращая внимания на процесс обработки (рис. 68).

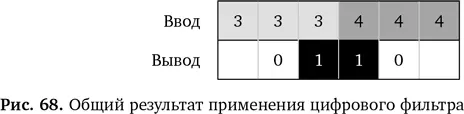
После фильтра на выходе числа оказались больше только там, где была замена значений на входе. Конечно, результат на выходе немного меньше, чем изображение на входе, ведь два значения оказываются пустыми. Однако он гораздо полезнее. Вместо того чтобы считать эти значения на входе в виде цифр, представьте их в виде пикселов. Это картинка.

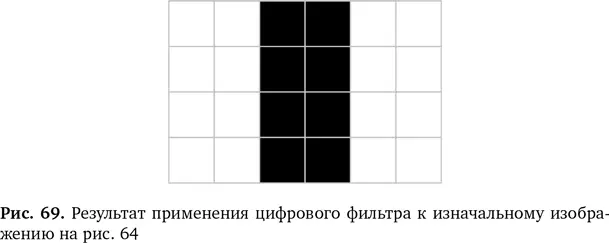
Теперь подумайте, что происходит, когда вы прогоняете через этот фильтр первую строчку нашего скучного изображения на рис. 64, затем продвигаетесь ниже и проходите следующую, а затем и еще одну строку, пока не отфильтруете все изображение на входе. У вас получится новое изображение немного меньшего размера, как на рис. 69, где мы приняли 0 для белого и 1 для черного. У него есть особое свойства. Все области, где были вертикальные границы, оказались выделенными — они стали линиями. Немного математики, и из исходного изображения возник новый шаблон. Границы превратились в линии, и теперь компьютер их видит.

Программисты изобрели много разных фильтров, каждый из которых может обнаружить в изображениях разные элементы. За этим стоит тот же математический процесс, который мы только что рассмотрели. Правда, сами фильтры становятся все сложнее. Каждый из них — это шаблон. Использование шаблонов в фильтрах является основополагающим элементом компьютерного «зрения» при поиске закономерностей в изображениях. Кроме того, таким образом мы имитируем все, что знаем о человеческом зрении: похоже, что у клеток человеческого мозга есть определенные закономерности восприятия изменений интенсивности света, а это и есть линии.

Важные закономерности проявляются и во времени. Для этого мы создаем ПО, которое наблюдает за людьми, отслеживая выражение лица, и за предметами, которые двигаются и меняются. Для компьютера видео не более чем большой набор чисел. Оно состоит из последовательности картинок, снятых в течение определенного времени, а, как мы уже говорили, каждое изображение — это и есть набор чисел. Чтобы найти в видео интересные вещи, нужно эти числа фильтровать. Можно создать фильтры, которые работают не только во времени, но и в пространстве. Это так называемые временные фильтры —они ищут сходство или различие в значениях пикселов в конкретных участках видеоизображений по ходу фильма. Возьмем фильтр из нашего примера [ −1, 0, +1]. Он представляет собой маленькую компактную абстракциютого, что мы хотим найти. У него те же характеристики, что и у границы, — он начинается с меньшего значения и заканчивается наибольшим.

Когда нам нужно проследить за более сложными моделями во времени, мы порой слабо представляем, что это за модели, поэтому трудно создать исходный фильтр. Чтобы решить эту проблему, обычно используют алгоритмы, способные изучить необходимые нам модели. Это подразумевает создание фильтров на основе сотен образцов. Такие фильтры бывают очень сложными. Например, можно взять сотни видео с обычным поведением людей, входящих в поезд метро и выходящих из него, и извлечь из них наиболее вероятные модели. Если прогнать через эти усвоенные фильтры настоящую сцену, происходящую на платформе, они выделят подозрительное поведение. Это могут быть модели движения, которые мы не ожидаем здесь увидеть, — например, кто-то слишком долго ждет у края платформы или на ней стоит сумка, которую никто не забирает. То есть мы увидим исключения из изученных моделей.