Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

В томографии это будет форма внутренних органов тела, изображения которых можно записать во всем их трехмерном великолепии. Сейчас существуют системы, в которых излучатель вращается вокруг тела по спирали, что ускоряет процесс. Можно даже снять в разрезе бьющееся сердце и оценить его работу. Математическое основание этой технологии называется преобразование Радона —по имени чешского математика Иоганна Радона, который умер в 1956 г. Оно было разработано как абстрактная математическая теория. В то время никто не видел для нее применения!

Пока вы думаете, как превратить плоские снимки в трехмерное изображение тела, давайте сделаем перерыв и сыграем в морской бой. Это еще одна простая игра на основе сетки, для которой понадобятся карандаш и бумага. Играют вдвоем. Каждый игрок рисует сетку, помечает на ней ряды и столбцы и решает, в каких клетках расположить корабли. Флот состоит из кораблей разного типа: линкор обычно занимает четыре клетки по горизонтали или по вертикали, крейсер (меньший по размеру корабль) занимает, скажем, только две клетки, а эсминец — одну. Сначала вы решаете, сколько кораблей каждого типа будет в игре, и располагаете их на решетке втайне друг от друга. По правилам вы по очереди «бьете» по решетке вашего противника. Например, противник бьет по позиции В9. Это квадрат в строке B и столбце 9. Если эту клетку занимает часть вашего корабля, он «ранен». Вы должны сказать, какой это корабль, и противник делает следующий ход. Таким образом можно попытаться понять, расположен ли четырехклеточный корабль горизонтально или вертикально. Первый игрок, который потопит весь флот противника, побеждает. Конечно же, труднее всего попасть по эсминцам, которые занимают одну клетку, ведь для этого нужно попасть точно в цель.

Теперь представьте гораздо менее масштабную игру, как на рис. 70 а. Это скорее не океан, а пруд. В нем только один эсминец (он обозначен цифрой 1 в море нолей) на позиции В2. Может быть, вам повезет, и вы попадете по B2 с первого же выстрела. Но весьма вероятно, что придется долго исключать разные варианты, прежде чем вы его найдете. Есть ли другой способ найти 1?

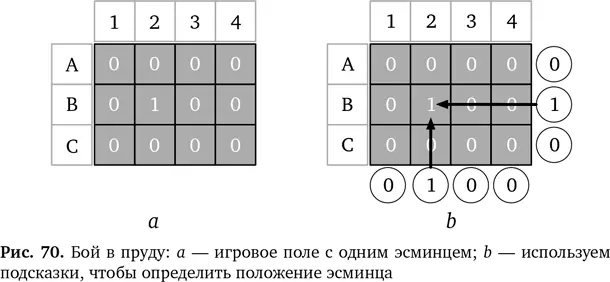
Да, такой способ есть, но только если противник даст вам кое-какие простые подсказки. Тогда вы сможете догадаться. Во-первых, нужно, чтобы второй игрок сложил значения клеток в каждой строке и сообщил их. Для ситуации как на рис. 70 aинформация будет такой: 0 в строке A (потому что там 0 + 0 + 0 + 0, хотя вам скажут только про 0 в сумме), 1 в строке B (потому что там 0 + 1 + 0 + 0) и 0 в строке С. Это начало. Теперь вы знаете, что корабль находится в строке B, но не знаете, где именно. Теперь спросите, какая сумма получается в каждом столбце. В столбце 1 выходит 0, в столбце 2 — 1, в столбце 3 — 0 и в столбце 4 — 0. Теперь вы знаете, что корабль находится в столбце 2. Это показано на рис. 70 b, где подсказки расположены в кружочках по краям игрового поля. Обобщив эту информацию, вы поймете, что корабль находится в клетке В2, и — БАБАХ! — он потоплен!

Теперь представьте, что где-то в сетке располагаются два эсминца. На этот раз мы не скажем, где они. Ваш друг снова сообщает вам сумму значений в каждой строке и столбце. На этот раз вы узнаете, что у вас есть 2 в строке А, 0 в строке В и 0 в строке C; 1 в столбце 1, 0 в столбце 2, 1 в столбце 3 и 0 в столбце 4, как на рис. 71a. Где же корабли?

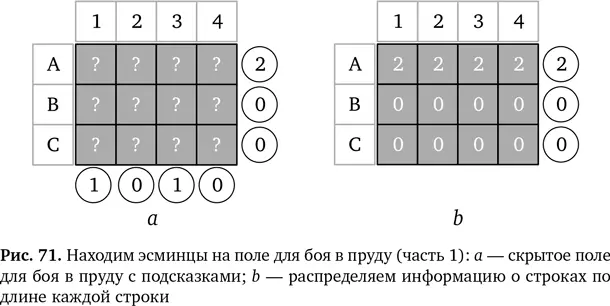
Вот общий подход к поиску кораблей. Во-первых, нам сказали, что в строке А сумма равна 2. Значит, там что-то есть! Мы можем распространить информацию о присутствии чего-то на всю строку А до самого конца. Хотя мы распределили данные по всей строке, мы все еще не знаем, где находится «что-то», а просто уверены, что оно где-то там есть. Давайте продолжать. Теперь распределим данные по строкам В и С. Здесь нет дополнительной информации, потому что в каждой строке стоит по нолю. В результате получается сетка как на рис. 71 b.

Мы знаем, что в строке А что-то есть, это здесь и показано. Но пока мы не знаем, что же это такое. Теперь мы смотрим на столбцы и создаем новую сетку. Если так же распределить информацию по столбцам, где в столбце 1 будет 1, в столбце 2 — 0, в столбце 3 — 1 и в столбце 4 — 0, то получится сетка как на рис. 72 a.

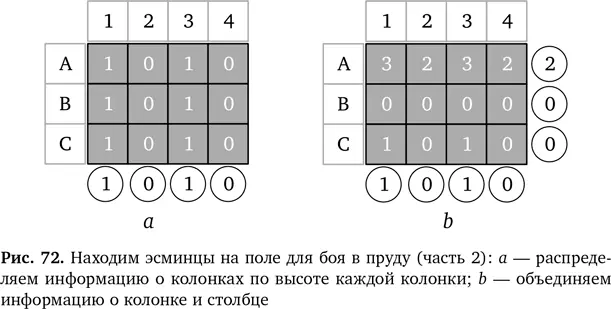
Мы знаем, что в столбцах 1 и 3 что-то есть, но не знаем, где именно. Чтобы окончательно решить эту задачу и восстановить расположение кораблей, мы просто складываем эти сетки с распределенной информацией вместе и получаем сетку как на рис. 72 b.

В объединенной сетке, например, A1 = 2 + 1 = 3, A2 = 2 + 0 = 2, A3 = 2 + 1 = 3 и так далее. Если теперь посмотреть на эту объединенную сетку с двумя наборами распределенных данных, то мы увидим на ней два пиковых значения 3 на позициях A1 и A3. Эти пиковые значения и отмечают, где находятся корабли. Итак, у нас есть автоматический детектор кораблей, но, что еще важнее, есть и способ открыть истинное расположение кораблей на сетке. Мы можем восстановить, как выглядит наш пруд, по одним подсказкам — см. рис. 73. Чтобы этого добиться, нужно использовать результаты, которые получаются при сложении всех данных в строке и в столбце. Теперь пришло время сняться с якоря и вернуться к рентгеновским лучам. Как вы, вероятно, догадались, все это время мы занимались задачей, связанной именно с ними.

Рентгеновский луч, проходя сквозь тело, поглощается костной тканью. Поэтому в конкретной точке рентгенографической пластины мы получаем нечто похоже на объединение всех «кораблей» (участки, занятые костной тканью) на пути рентгеновского луча (можно сказать, на строке игрового поля). Итак, наш рентгеновский луч похож на последовательность чисел: строка А = 2, строка B = 0 и строка C = 0. Мы знаем, что луч, поступающий в позицию А, прошел через большее число костей (кораблей), чем лучи, прошедшие через B или C. Но мы хотим знать, как эти кости расположены по отношению друг к другу. Находятся ли они близко или же далеко? В обоих случаях рентгеновское излучение будет поглощено в одном и том же объеме. Но можно вращать источник рентгеновского излучения, как и наш детектор кораблей, вокруг пациента, начиная сверху, а не сбоку, и сделать еще один снимок. На этот раз на рентгенографической пластинке появится информация о форме: колонка 1 = 1, колонка 2 = 0, колонка 3 = 1 и колонка 4 = 0.