Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0…βm , потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):

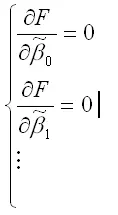
где

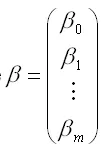
– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1 );

Общий вид стационарной системы уравнений для функции (1):

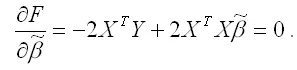
Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии:

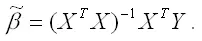
Оценим с помощью метода наименьших квадратов неизвестные параметры линейной модели двухфакторной регрессии:

yi=β0+β1x1i+β2x2i+εi,

где

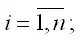
Чтобы рассчитать оценки неизвестных коэффициентов β0,β1 и β2 данной двухфакторной модели регрессии, необходимо минимизировать функционал F вида:

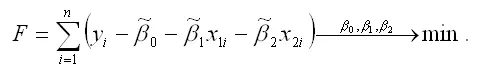
Для определения экстремума функции нескольких переменных, частные производные по этим переменным приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для модели множественной линейной регрессии с двумя переменными:

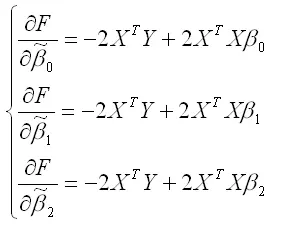
В результате элементарных преобразований данной стационарной системы уравнений получим систему нормальных уравнений:

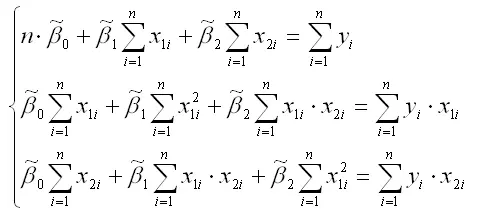
Данная система называется системой нормальных уравнений относительно коэффициентов

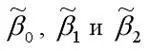
для модели регрессии yi=β0+β1x1i+β2x2i+εi.

Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты

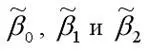
можно рассчитать с помощью метода Крамера или метода Гаусса .

Рассмотрим подробнее метод Крамера решения квадратных систем нормальных уравнений.

Единственное решение квадратной системы линейных уравнений определяется по формуле:

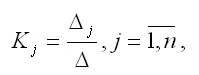
где Δ – основной определитель квадратной системы линейных уравнений;

Δ j – определитель, полученный из основного определителя путём замены j-го столбца на столбец свободных членов.

При использовании метода Крамера возможно возникновение следующих ситуаций:

1) если основной определитель системы Δ равен нулю и все определители Δj также равны нулю, то данная система имеет бесконечное множество решений;

2) если основной определитель системы Δ равен нулю и хотя бы один из определителей Δj также равен нулю, то система решений не имеет.

Помимо классического метода наименьших квадратов для определения неизвестных параметров линейной модели множественной регрессии β0…βm используется метод оценки данных параметров через β -коэффициенты (коэффициенты модели регрессии в стандартных масштабах).

Построение модели множественной регрессиив стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.

Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение σ .

Факторная переменная х переводится в стандартизированный масштаб по формуле:

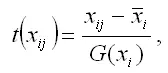
где xij – значение переменной xj в i -том наблюдении;

G(xj) – среднеквадратическое отклонение факторной переменной xi ;

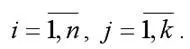
Результативная переменная у переводится в стандартизированный масштаб по формуле:

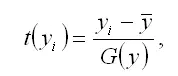
где G(y) – среднеквадратическое отклонение результативной переменной у .

Если между исследуемыми переменными в исходном масштабе является линейной, то процесс стандартизации не нарушает этой связи, поэтому стандартизированные переменные будут связаны между собой линейно:

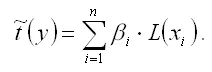
Неизвестные коэффициенты данной функции можно определить с помощью классического метода наименьших квадратов для линейной модели множественной регрессии. В этом случае минимизируется функционал F вида:

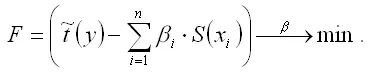
В результате минимизации данного функционала получим систему нормальных уравнений, переменными в которой будут являться парные коэффициенты корреляции между факторными и результативной переменной. Такой подход основывается на следующем равенстве:

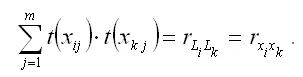
Система нормальных уравнений для стандартизированной модели множественной регрессии имеет вид: