Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

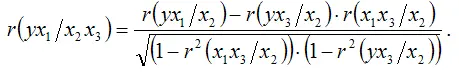
Частный коэффициент корреляции между результативной переменной у и факторной переменной х2 при постоянстве факторных переменных х1 и х3 :

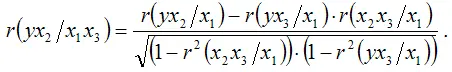
Частный коэффициент корреляции между результативной переменной у и факторной переменной х3 при постоянстве факторных переменных х1 и х1 :

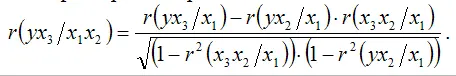
Частные коэффициенты корреляции второго порядка построены с использованием частных коэффициентов корреляции первого порядка.

Следовательно, частный коэффициент корреляции порядка t может быть построен через частный коэффициент корреляции ( t-1 ) порядка. Формулы, построенные через указанную взаимосвязь, называются рекуррентными.

При анализе модели множественной регрессии с n факторными переменными, частный коэффициент корреляции ( n-1 ) порядка рассчитывается по общей формуле:

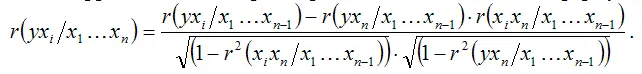
Частные коэффициенты корреляции, вычисленные по рекуррентным формулам, изменяются в пределах от минус единицы до плюс единицы.

Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для моделей множественной регрессии, возможно также построение этих показателей с помощью показателя остаточной дисперсии.

В случае линейной модели парной регрессии показатель остаточной дисперсии определяется по формуле:

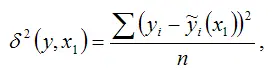
где

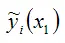
– это оценка модели парной регрессии с независимой переменной х1 .

Если в линейную модель парной регрессии включить новую независимую переменную х2 , то можно вычислить показатель остаточной дисперсии для линейной модели регрессии с двумя независимыми переменными:

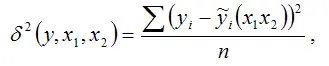
где

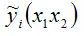
– это оценка модели регрессии с двумя независимыми переменными х1 и х2.

Вне зависимости от качества построенной линейной модели двухфакторной регрессии будет справедливо неравенство вида:

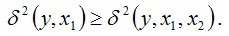
Тогда величину

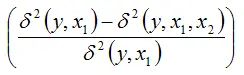
можно охарактеризовать как долю сокращения остаточной дисперсии за счёт включения в модель регрессии новой независимой переменной х2 . Чем больше величина данного показателя, тем сильнее дополнительная переменная х2 влияет на результативную переменную у и на качество модели регрессии в целом.

Для линейной модели двухфакторной регрессии частный коэффициент корреляции между независимой переменной х2 и результативной переменной у при постоянном значении независимой переменной х1 через показатель остаточной дисперсии определяется по формуле:

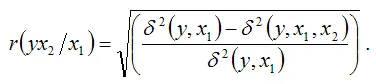
Для модели множественной регрессии с n независимыми переменными частный коэффициент корреляции ( n-1 ) порядка независимой переменной х1 и результативной переменной у при постоянном значении остальных независимых переменных, включённых в модель, определяется по формуле:

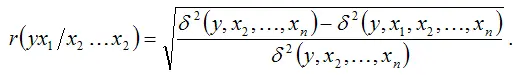
Показатель остаточной дисперсии результативной переменной и коэффициент множественной детерминации связаны отношением:

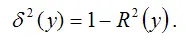
Если в формуле частного коэффициента корреляции выразить остаточную дисперсию результативной переменной с помощью коэффициента множественной детерминации, то для модели множественной регрессии с n независимыми переменными частный коэффициент корреляции в общем виде можно определить по формуле:

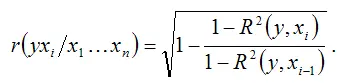
Частные коэффициенты корреляции, вычисленные через показатель остаточной дисперсии или коэффициент множественной детерминации, изменяются в пределах от нуля до единицы.

Частный коэффициент корреляции для модели множественной регрессии в общем случае характеризует степень зависимости между результативной переменной и одной из факторных переменных при постоянном значении остальных независимых переменных, включённых в модель регрессии.

Если частные коэффициенты корреляции модели множественной регрессии оказались значимыми, т. е. между результативной переменной и факторными модельными переменными действительно существует корреляционная взаимосвязь, то в этом случае построение множественного коэффициента корреляции считается целесообразным.

С помощью множественного коэффициента корреляции характеризуется совокупное влияние всех факторных переменных на результативную переменную в модели множественной регрессии.

Коэффициент множественной корреляции для линейной модели множественной регрессии с n факторными переменными рассчитывается через стандартизированные частные коэффициенты регрессии и парные коэффициенты корреляции по формуле:

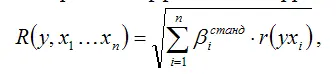
где r (yxi) – парный (не частный) коэффициент корреляции между результативной переменной у и факторной переменной xi

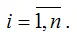
Коэффициент множественной корреляции изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение множественного коэффициента корреляции к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение множественного коэффициента корреляции к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.