Морис Котрелл - Сверхбоги

Для измерения временных периодов использовались следующие циклы истекшего времени: 144 000, 7200, 360, 20 и 1 день.

Как только система числового кодирования была раскрыта, эти циклы указали на период катастроф 1 366 560 дней.

Дальнейшее изучение чисел показывает, что система счисления прерывается после 1 366 560 дней и что для продолжения «счета» систему необходимо адаптировать. Адаптация свидетельствует об использовании десятичной системы (М. Котрелл. «Пророчества майя»).

Было проведено немало экспериментов с целью определить человеческие предпочтения в формах и пропорциях. Наиболее предпочтительным из всех соотношений является золотое сечение. Оно не только доставляет эстетическое удовольствие, но и совместимо с человеческой психологией, которая, как мы увидим, также связана с золотым сечением. Изображенная ниже фигура представляет собой прямоугольник. Отношение его длинной стороны к короткой дает нам число золотого сечения, равное 1,6180339.

Это число, обладающее многими удивительными свойствами, первым открыл Евклид около 300 г. до н. э. У математиков его принято обозначать греческой буквой Ф (фи). Художники эпохи Возрождения называли его «божественной пропорцией», а греки использовали пятиугольник (который содержит множество соотношений, основанных на Ф) как священный символ. Ф также имеет множество важных математических значений; все живые организмы, такие, как человеческое тело, растения, животные, связаны с Ф. Таким образом, отдавая предпочтение основанным на Ф пропорциям, мы подчиняемся законам природы и реагируем на то, что, по всей видимости, является уникальным кодом, связанным с нашей собственной структурой.

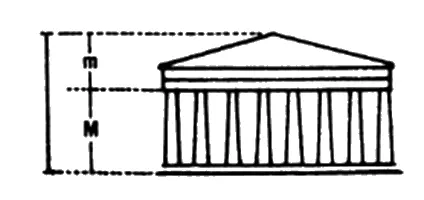
Художники всегда стремились соблюсти пропорции золотого сечения в своих работах: например, линия горизонта на картине редко делит холст, скажем, 50 на 50, а обычно делает это в соотношении близком к Ф, то есть 1,62:1.

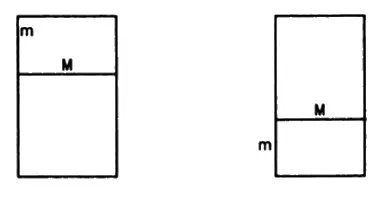
У изображенных выше прямоугольников соотношение сторон 1,618:1. Эти прямоугольники обладают целым рядом любопытных особенностей. Если вы построите квадрат, на его длинной стороне, как показано здесь, этот квадрат, вместе с прямоугольником, образует новый, больший по размерам Ф-прямоугольник. Соотношение между длинной стороной М и короткой стороной m такое же, как соотношение между длинной и короткой сторонами большого прямоугольника. Это математическая пропорция. Ф содержит также и арифметическое соотношение. Если вы разделите 1 на Ф, то получите 0,618. Если вы умножите Ф на само себя, то результатом будет 2,618. Сравните эти два числа с Ф, и вы заметите нечто странное в их соотношении.

В тринадцатом веке математик Фибоначчи открыл интересную и загадочную последовательность чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… После того как серия начинается с 1,1, каждый новый член этой последовательности получается в результате сложения двух предыдущих. Однако если взять любую пару из двух соседних чисел и разделить большее число на меньшее, то результатом будет число, близкое к Ф.

Мы видим, что эта серия чередуется, постепенно приближаясь к числу 1,6180339: чем больше числа, тем ближе их частное к Ф. Последовательность Фибоначчи, которая является функцией Ф, доминирует в природе, как и само Ф.

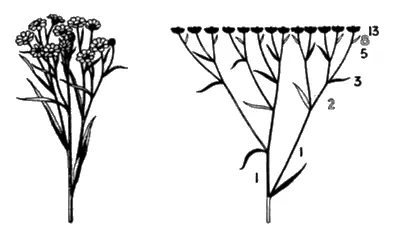
Никто не скажет, что растение, изображенное на рисунке 86а, имеет какое-то отношение к математике; оно кажется слишком неорганизованным и несимметричным. Но простое исследование его структуры и особенностей роста (рис. 86б) сразу же позволяет обнаружить последовательность Фибоначчи.

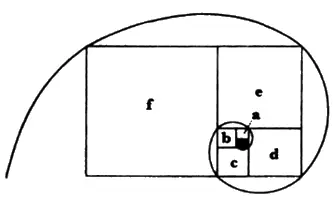
На рисунке 87 квадрат а был добавлен к маленькому черному прямоугольнику, расположенному в центре, так же, как это было продемонстрировано на рис. 83. Вместе они образовали больший по размерам прямоугольник с пропорциями золотого сечения. Если вы теперь добавите к большой стороне нового прямоугольника еще один квадрат, b, то получите еще один Ф-прямоугольник. Вы можете продолжить делать это с квадратами с, d, е и f. Если соединить углы всех прямоугольников, то в результате мы получим спираль, которую можно встретить во многих естественных формах.

Эти формы проявляются и во многих других аспектах жизни, например в сосновой шишке и в цветке георгина, которые имеют по два набора спиралей, связанных с последовательностью Фибоначчи.

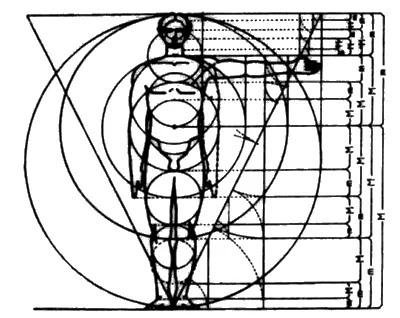
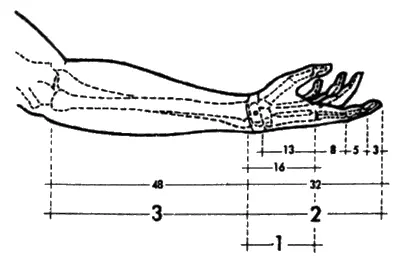
Кроме природных спиралей, числа Фибоначчи играют важную роль и в пропорциях человеческого тела (рис. 90). Природа наполнена такими соотношениями. В большинстве случаев их можно только почувствовать, но здесь мы видим некоторые из них, выраженные в числах и математических терминах.

Ф наполняет собой все живые существа.

Агни

Арийский бог огня, сын Дьяуса и Притхиви, бог юго-восточного квадранта неба.

Адити

Брахманская богиня, жена Брахмы.

Ананта

Брахманский змей бесконечности.

Арджуна

Воин, главный персонаж индуистской «Бхагавад-гиты»

Астеки

Раса центральноамериканских индейцев, принадлежащих к языковой группе науатль, период расцвета 1300–1520 гг. н. э.