Друнвало Мельхиседек - Древняя Тайна Цветка Жизни. Том 1

Представьте, что этот маленький центральный круг есть планета в пространстве космоса. С поверхности планеты автор учебника по математике вычертил спираль Золотого Сечения – не Фибоначчи, но Золотого Сечения. Она начинается в нулевом радиусе на поверхности маленькой «планеты» в середине, и описывает один оборот, от нуля до 360 градусов, или назад к нулю

Теперь, чтобы определить значение каждой точки спирали, вы используете средний круг в качестве единицы (поскольку он представляет расстояние от центра к первой окружности, которую мы назвали «планетой»), и затем отсчитываете единицы наружу до того места, где спираль пересекает радиус. Так, на радиусе в 260° (между четвёртым и пятым кругами) вы отсчитали наружу примерно 4,5. (Конечно, на компьютере вы можете сделать это точнее.) На радиальной линии в 210° спираль достигала почти 3,3. Все ли это поняли?

Теперь смотрите, что происходит с конкретными значениями от нуля до 360°. При нулевом градусе спираль находится точно на расстоянии одного круга (радиальное возрастание) от центра, поскольку она начинается с поверхности маленькой сферы или планеты. Затем она делает оборот, проходя через различные изменения до тех пор, пока не достигает 120°, где спираль пересекает второй круг. Она продолжает движение наружу к пересечению с четвёртым кругом точно там, где располагается радиальная линия 240°. И восьмого (внешнего) круга она достигает точно у радиуса 360° (или 0°). Радиальные возрастания удваивались (бинарная последовательность 1,2,4,8) точно в 0°,120°,240° и 360°.

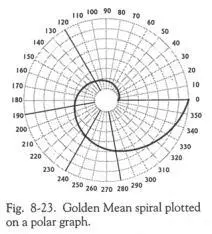
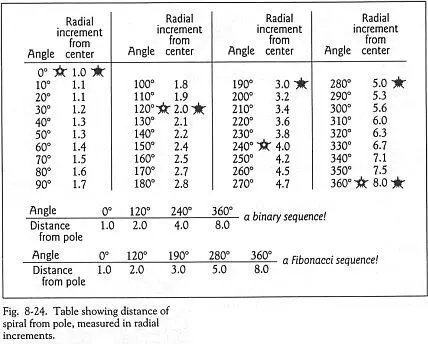
Обратите внимание на Рис.8-24, где показаны точки пересечения спирали. Белые звёздочки слева от столбика радиального возрастания показывают, где бинарная последовательность пересекает радиус. Чёрные звёздочки показывают, как спираль развивается по последовательности Фибоначчи (1,2,3,5,8), пересекая радиусы 120°, 190°, 280° и 360°. Обе последовательности одновременно достигают полного круга (360°), хотя и по различной линии возрастания , следуя этой спирали Золотого Сечения. Эта спираль, показанная на Полярном графике, интегрировала последовательности Фибоначчи и бинарную!

Я был так возбуждён, что несколько дней ходил колесом. Я знал, что обнаружил нечто действительно необычайное, хотя полностью ещё не понимал, что это такое. (Это одна из моих слабых сторон, в которой мне следует тут признаться. Однажды увидев это, я понял, что раз я расшифровал одну из закономерностей, это должно бы быть справедливо и для другой, но я никогда не возвращался к ней, чтобы хотя бы взглянуть на другую модель, которая, вероятно, так же интересна).

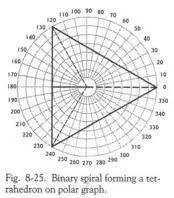
Но я в самом деле проанализировал, как ведёт себя бинарная последовательность. Спираль пересекается на 0°, 120°, 240° и 360°. Как видите, это даёт образование равнобедренного треугольника (Рис.8-25). Если бы эта бинарная спираль продолжала движение наружу, она пересекала бы радиусы в следующих возрастаниях по градусам 16, 32, 64 и так далее, однако всегда касалась бы этих трёх радиальных линий на 120, 240 и 360 градусах, так как они тоже продолжены.

Тут есть не только треугольник, но на самом деле вы глядите на трёхмерный тетраэдр, потому что радиусы 120, 240 и 360 градусов продолжаются к центру, образуя как план тетраэдра, так и его вид сбоку.

Новейшая информация: Была обнаружена ещё одна закономерность, которая, как я и подозревал, оказалась последовательностью Фибоначчи. Однако, я ещё не определил, какова значимость этого открытия для сознания.

Треугольники Кита Кричлоу (Keith Critchlow) и их музыкальное выражение

Ещё одна фигура этого чертежа представляет собой равнобедренный треугольник с горизонтальной линией, проходящей прямо через середину от 0° к 180°. Это боковой вид тетраэдра. Вы могли бы не придать этому значения, и я, наверное, никогда бы не догадался, но другой человек, Кит Кричлоу, это сделал. Нам неизвестно, что он думал и как он к этому пришёл. Когда он это сделал, он не знал того, что сейчас знаете вы. (Он мог узнать это теперь, после того, как он увидел эту работу, но когда он писал свою книгу, он этого не знал.)

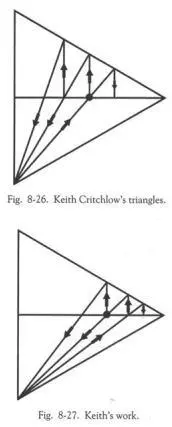
Рис.8-26 – это труд Кричлоу. Он начертил равносторонний треугольник с линией, проходящей через середину; затем он отмерил середину центральной линии (см. чёрную точку) и прочертил линию вниз к углу и вверх до края к верхней стороне, а затем вертикально вниз к центральной линии, как показано на рисунке. Кто знает, почему? Затем там, где эта первая диагональная линия пересекла центральную линию, он провёл вертикальную линию к верхнему краю, и опять провёл линию вниз к тому же нижнему углу. Воспользовавшись точкой пересечения этой диагонали с центральной линией, он снова провёл вертикальную линию к верхнему краю, и опять опустил линию вниз в нижний угол. Пользуясь точкой пересечения с центральной линией, он повторил всё, что делал прежде, а затем проделал то же самое налево. От первой линии можно продолжать двигаться так в обоих направлениях. Начертив эту забавную маленькую фигуру, он совершил очень важное открытие.

Он говорит: «Следуя этой схеме в данной строительной модели, каждая последующая пропорция становится гармоническим соотношением между предыдущей пропорцией и общей длиной, и все эти пропорции будут нести в себе музыкальное значение: одна вторая даёт октаву, две трети – квинту, четыре пятых -главную терцию, восемь девятых – основной тон (секунду) и шестнадцать семнадцатых – полушаг (полутон).» Иными словами, он сравнивает измерения этих линий с музыкальными тонами.

Затем он попробовал измерять иначе, начав с другой точки центральной линии (Рис.8-27), отметив три четверти (см. чёрную точку), и обнаружил, что расстояния составили 1/7, 1/4, 2/5, 4/7, 8/11 и 6/19 – и все это числа имеют музыкальное соответствие.

Это очень, очень интересно. Это значит, что музыкальные гармонии каким-то образом связаны с пропорциями этой центральной линии, проходящей через тетраэдр. Но Кричлоу начинал с измерения, и если вам всё ещё необходимо применять линейку, то значит, вы ещё не добралось до самых основ священной геометрии; чего-то не хватает. Если вы уже добрались до священной геометрии, тогда вам для измерения ничем никогда пользоваться не приходится. Измерительный аппарат уже встроен так, что возможно рассчитать всё, что угодно, не производя никаких вычислений и не пользуясь линейкой или чем бы то ни было. Это всегда уже встроено прямо в саму систему.