Сергей Доронин - Квантовая магия

Часто используется стандартный базис — из чисел в двоичной системе: 0…00, 0…01, 0…10, 0…11 и т. д. Так делается в компьютерах, где любая информация записывается в двоичном базисе.

Этот базис применяется и в физике: например, в случае спиновых степеней свободы каждая позиция соответствует двум возможным состояниям одного спина во внешнем магнитном поле (0-спин-вверх, 1-спин-вниз).

Сумма диагональных элементов, то есть след матрицы плотности равен единице. Так, в квантовой теории информации, когда пересылается какое-либо сообщение, возможны искажения, и получателю может прийти не то, что было послано: к примеру, вместо одной буквы — другая. Набор основных состояний системы (диагональные элементы матрицы плотности) характеризует все возможные варианты таких искажений (их вероятности), а «приемник» прочитает только один из них. То есть будет реализован один из искаженных вариантов с соответствующей вероятностью, а сумма вероятностей (след матрицы плотности) должен быть равен единице.

Еще одно важное свойство матрицы плотности — это ее эрмитовость . Попросту говоря, любая матрица плотности должна быть симметричной (в вещественном случае), ее недиагональные элементы расположены парами симметрично относительно главной диагонали. В комплексном случае эти пары будут комплексно сопряженными — это и есть эрмитоваматрица. Такая симметричная структура матрицы плотности является следствием того, что корреляции в системе всегда выступают парами: если одна подсистема взаимодействует с другой, то и вторая коррелируетс первой — это одно и то же взаимодействие. Только, когда речь идет о матрице плотности, более правильно говорить о наборе различных основных состояний системы (диагональные элементы) и о корреляциях между ними (недиагональные элементы). По диагонали матрицы плотности стоят вероятности «проявления» дискретных состояний при декогеренции (в случае исходного нелокального состояния). Например, у кубита два локальных состояния 0 и 1, их вероятности — это | a | 2и | b | 2, то есть существует бесконечное число различных вариантов весовых соотношений при наложении (суперпозиции) этих двух состояний. А недиагональные элементы характеризуют корреляции между данными основными состояниями, в случае кубита — это ab *и ba *, звездочка здесь — знак комплексного сопряжения. Пространство состояний для матрицы плотности — не только набор всех дискретных (базисных) состояний, это и все возможные корреляции между ними. Полный набор возможных локальных состояний — лишь диагональные элементы матрицы плотности. Из-за того, что учитываются все возможные связи между состояниями, число элементов в матрице плотности увеличивается экспоненциально с числом кубитов N и равно 2 N × 2 N .

Другое свойство любой матрицы плотности — ее положительная полуопределенность . Все собственные значения матрицы плотности вещественны (нет комплексных чисел) и неотрицательны (больше нуля или равны ему). Для матрицы плотности всегда существует унитарное преобразование, которое приводит ее к диагональной форме, и по диагонали будут стоять неотрицательные вещественные числа. В случае чистых состояний ситуация еще проще — матрица плотности такого состояния имеет только одно ненулевое собственное значение (равное единице), а все остальные равны нулю.

На простом примере я попытаюсь показать, как строится матрица плотности. Рассмотрим систему, состоящую из двух частей ( А и B ), каждая из которых может находиться в двух состояниях 0 и 1. Вектор типа |01ñ означает, что подсистема А находится в состоянии 0 (пусть она стоит на первой позиции), а подсистема B — в состоянии 1.

Если система замкнута (чистое состояние), то мы можем записать для нее вектор состояния, например, в стандартном базисе:

|Ψñ = a |00ñ + b |01ñ + c |10ñ + d |11ñ, (3.1)

где a, b, c, d — в общем случае комплексные числа (амплитуды) и выполняется условие нормировки | a | 2+ | b | 2+ | c | 2+ | d | 2= 1.

Вектор состояния (3.1) описывает все возможные состояния системы, и их бесконечное число, поскольку амплитуды заданы на множестве комплексных чисел. То есть a, b, c, d могут быть любыми числами (удовлетворяющими условию нормировки), как вещественными, так и комплексными, и таких чисел бесконечно много.

Матрица плотности для чистого состояния записывается как проектор |ΨñáΨ| (вектор-столбец (3.1) нужно умножить на комплексно сопряженную строку). Это матрица 4 × 4 и по диагонали в ней стоят | a | 2, | b | 2, | c | 2, | d | 2— это вероятности нахождения системы в каждом из четырех возможных собственных состояний |00ñ, |01ñ, |10ñ, |11ñ соответственно. Сумма вероятностей этих состояний (след матрицы плотности) равна 1 (условие нормировки). Недиагональные элементы характеризуют корреляции (взаимодействия) между четырьмя различными состояниями системы, в них содержится информация о градиентах энергии, возникающих в ней.

Состояние (3.1) может быть максимально запутанным, например, одно из них:

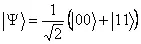. (3.2)

Матрица плотности в этом случае равна:

. (3.3)

То есть система с равной вероятностью 1/2 находитсяв состояниях |00ñ и |11ñ («кот ни жив, ни мертв») — это диагональные элементы. И корреляции между этими состояниями максимальны (недиагональные элементы). Мы видим, что недиагональные элементы равны друг другу и расположены симметрично, как и должно быть для любой матрицы плотности.

При измерении этого нелокального состояния (при декогеренции) мы получим одно из двух классических локальных (сепарабельных) состояний |00ñ или |11ñ с равной вероятностью.

Существует простой способ проверить, относится ли какая-либо матрица плотности к чистому состоянию или нет. Если умножить матрицу саму на себя, и она при этом не изменится (получится та же самая матрица), то есть если выполняется равенство ρ 2= ρ , то можно сразу сказать, что данная матрица плотности описывает чистое состояние, и для него может быть записан вектор состояния. Такие матрицы, которые не меняются при умножении самой на себя, называются идемпотентными. Таким образом, любая матрица плотности чистого состояния — идемпотентная.

Если система незамкнутая (открытая), то это смешанное состояние, и тогда она не описывается вектором состояния, но ее по-прежнему можно описать матрицей плотности. Например, максимально смешанное состояние:

. (3.4)