Сергей Доронин - Квантовая магия

P x = sin θ cos φ ,

P y = sin θ sin φ ,

P z = cos θ ,

и два вещественных параметра (углы θ и φ ) однозначно задают вектор состояния (матрицу плотности) кубита.

В случае смешанного состояния длина вектора поляризации становится меньше единицы, то есть 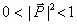, и он будет расположен внутри сферы.

Итак, матрица плотности кубита может быть представлена точкой в нашем привычном трехмерном пространстве. То есть существует взаимно однозначное соответствие между матрицей плотности и точкой шара единичного радиуса. Для чистого состояния (замкнутой системы) — это точка сферы.

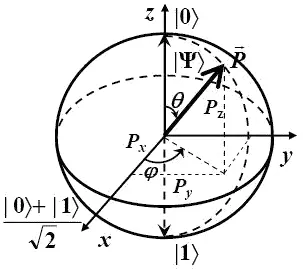
Чистые состояния, описываемые одним вектором состояния, соответствуют точкам поверхности сферы Блоха, а смешанные состояния, описываемые матрицей плотности, — точкам внутри шара. При взаимодействии с окружением (при декогеренции), в случае смешанного состояния, вектор состояния как бы погружается внутрь сферы Блоха ибудет описывать уже не окружность, а, например эллипс, что-то похожее на форму яйца. А в самом предельном случае, когда состояние кубита становится максимально смешанным, весь шар, все пространство допустимых состояний, сжимается до отрезка на оси квантования между значениями 1/2 и —1/2. Этот отрезок — тот минимум, который может остаться от кубита, скажем, в самом худшем (или лучшем?) случае.

Такая ситуация, например, имеет место при максимально запутанном состоянии сдругим кубитом. Тогда, как уже говорилось выше [см. выражение (3.5)], матрица плотности одного кубита является максимально смешанной.

В этом проявляется двойственный характер декогеренции: с одной стороны, она приводит к локализации системы, нарушению когерентного состояния, но с другой — взаимодействие с окружением ведет к квантовой запутанности с этим окружением. Можно еще сказать и так: предельно возможнаядекогеренция окружением совпадает с максимальной запутанностью с этим окружением. И реализуется эта ситуация при наличии максимально возможного взаимодействия между кубитами (как в нашем случае), когда они составляют единое целое (максимально запутанное состояние).

Можно задать вопрос: а какое количество информации содержит один кубит? Если с каждой точкой на сфере Блоха, с каждым положением вектора состояния сопоставить определенную информацию, то, как это ни парадоксально звучит, кубитсодержит бесконечный объем информации, и эта информация аналоговая, непрерывная. Кубит, двигаясь по поверхности сферы Блоха, непрерывно изменяет свое состояние, изменяя при этом информацию. Но информация, содержащаяся в кубите, — квантовая . «Считать» с кубита можно только один бит классической информации — либо 0, либо 1.

Одно из хорошо известных достоин ств квантовой теории заключается в том, что она может одновременно, в едином ключе, описывать как дискретные, так и непрерывные характеристики системы. Так же и в случае кубита. Имея два основных состояния, мы можем описать бесконечное число «оттенков» между этими двумя пограничными состояниями.

Управлять состоянием кубита — значит, управлять амплитудами а и b в векторе состояния, эти величины непрерывные, аналоговые, поэтому квантовый компьютер иногда называют компьютером с аналоговым управлением [94]. В настоящее время такое управление кубитами научились реализовывать унитарными (обратимыми) операциями. Попросту говоря, научились вращать вектор состояния кубита по сфере Блоха, переводя его в нужное состояние, в том числе в нелокальное суперпозиционное или в запутанное с другими кубитами.

При этом привычные для нас классические состояния кубита составляют бесконечно малую часть его совокупного пространства состояний. В терминах коэффициентов а и b — из бесконечного их числа только два значения соответствуют чистым классическим (локальным) состояниям, когда либо b = 0, либо a = 0 (в этом случае нет суперпозиции состояний, и у нас |Ψñ = |0ñ или |Ψñ = |1ñ). На сфере Блоха — это только две точки (полюсы) из бесконечного числа других точек сферы. Максимально запутанные состояния — точки экватора, это уже линия, а не две точки.

То же самое можно сказать и о любых объектах окружающей реальности. Их допустимое пространство состояний гораздо шире классических состояний. Классический домен составляет лишь незначительную (бесконечно малую) часть совокупной квантовой реальности окружающего мира.

В частных случаях, как я уже отмечал, состояниями кубитов можно управлять и целенаправленно получать любые состояния. Именно практическая работа над созданием квантовых компьютеров многое дала для понимания соотношений между различными состояниями и привела к реализации таких переходов. Например, ученые научились переводить кубиты из классического локального состояния в нелокальную суперпозицию (преобразование Адамара):

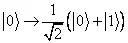или 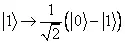. (3.13)

Можно назвать этот процесс рекогеренцией. Обратное преобразование (справа налево) — это декогеренция. И все эти «вращения» вектора состояния кубита по сфере Блоха можно делать при помощи унитарных преобразований, обратимых на временах, меньших времени декогеренции кубита внешним окружением.

Еще раз подчеркну, нелокальные суперпозиционные состояния и квантовую запутанность научились создавать для отдельныхкубитов. Такие «сверхъестественные» состояния уже невозможно объяснить ансамблевой интерпретацией, как это делал Эйнштейн, пытаясь уйти от «телепатии». Теперь эта «телепатия» между кубитами выходит на первый план и становится основным рабочим ресурсом в квантовой информатике.

Квантовая теория помогает глубже вникнуть в смысл некоторых хорошо известных понятий, которыми оперируют эзотерическая литература и восточная философия. Это относится, например, к понятию Инь/Ян, которое тщетно пытается охватить западный рациональный ум с целью вписать в рамки классических представлений, в то время как в терминах квантовой теории эта неуловимая двойственность выражается очень просто: Инь/Ян — это когерентная суперпозиция двух альтернативных состояний.

Очень многое свидетельствует в пользу того, что Инь/Ян соответствуют простейшему случаю двухуровневой системы в квантовой механике, то есть системы с двумя ортогональными состояниями (например, с максимальной и минимальной энергией). Это и есть описание в терминах кубита (как вектора состояния двухуровневой системы) в виде суперпозиции двух взаимоисключающих состояний. С одной стороны, Инь/Ян составляют единое целое, и одно из них невозможно выразить через другое. Но, с другой стороны, можно говорить об их корреляциях, о возможности их перераспределения в системе, о переходах между уровнями, о «шевелении» коэффициентами-амплитудами в векторе состояния, то есть о движении вектора состояния кубита по сфере Блоха.