Сергей Доронин - Квантовая магия

Рассмотрим эти уравнения. Они получаются из (5.1) разделением на пространственные и временные производные:

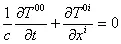, (5.2)

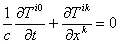. (5.3)

Эти уравнения затем интегрируются по некоторому произвольному объему пространства V , и применяется теорема Гаусса.

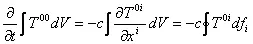, (5.4)

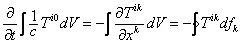. (5.5)

Интеграл справа берется по поверхности, охватывающей объем V ( df 1, df 2, df 3— компоненты трехмерного вектора элемента поверхности d f ).

Рассмотрим более подробно второе уравнение (5.5), поскольку результаты, полученные при его анализе, будут широко использоваться в дальнейшем.

Левая часть не вызывает вопросов — здесь стоит скорость изменения импульса в объеме V , то есть сила, действующая на этот объем. А вот в правой части мы перейдем к энергетическому представлению и для этого воспользуемся аппаратом дифференциальной геометрии, теоретические основы которого изложены в книге Б. А. Дубровина, С. П. Новикова, А. Т. Фоменко «Современная геометрия: Методы и приложения» (М.: Наука, 1986). Достаточно подробное описание того, как эти методы применяются в физике, в частности, к тензору энергии-импульса, содержится в книге Ч. Мизнера, К. Торна, Дж. Уилера«Гравитация», т. 1 (М.: Мир, 1977).

Очень кратко напомню смысл основных понятий дифференциальной геометрии, которыми нам придется оперировать. Прежде всегоэто касается еще одного геометрического объекта — «дифференциальной формы», который наряду с другими хорошо известными геометрическими объектами (скаляр, вектор, тензор) описывает физические величины. В частности, более подробно рассмотрим понятие 1-формы.

Может возникнуть закономерный вопрос: зачем вообще нужны дифференциальные формы, и нельзя ли обойтись хорошо известными старыми понятиями? Чтобы ответить на этот вопрос, приведу следующий пример из книги Мизнера-Торна-Уилера.

Рассмотрим привычное определение вектора 4-импульса pдля частицы, например электрона, с массой m и вектором 4-скорости u, то есть p= m u . Кроме этого, в физике известен и другой подход к понятию импульса, при котором каждой частице приписывается волна де Бройля. Эта волна имеет самый непосредственный физический смысл, ее дифракция на кристаллической решетке позволяет определить не только длину волны, но и ту конфигурацию в пространстве, которую образуют поверхности равных целочисленных значений фазы. Конфигурация этих поверхностей дает простейшую иллюстрацию, которую удается найти для 1-формы. Определив эти поверхности посредством выражения ћ ´ фаза, получим «1 -форму импульса» .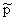

Посмотрим, что может дать такое представление импульса. Возьмем произвольный 4-вектор v. Он пересечет определенное число поверхностей целой фазы. Обозначим это число пересечений посредством выражения á 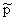, vñ. Как правило, началои конец вектора vне лежат на поверхностях целочисленных фаз. Чтобы определить более точное значение числа пересечений (перейти от целого числа к вещественному), необходимо в этих позициях между соседними поверхностями целой фазы распределить бесконечное число поверхностей со всеми промежуточными значениями фазы. Далее, чтобы понятие 1-формы стало рабочим инструментом, нужно сделать еще один небольшой шаг. Необходимо трактовать 1-форму не как глобальную конфигурацию поверхностей уровня, а как некоторую аппроксимацию этих поверхностей в элементарном, бесконечно малом объеме в виде плоских поверхностей, расположенных на равных расстояниях друг от друга (линейное приближение). Плоские поверхности 1-формы в этом малом объеме дадут наилучшую линейную аппроксимацию искривленных поверхностей уровня, а сама 1-форма становится линейной функцией , и появляется возможность оперировать ею, как и любой другой функцией. Нетрудно убедиться, что совокупность всех 1-форм в данном событии (4-точке) образует векторное пространство в абстрактном, алгебраическом смысле этого понятия. Существует и взаимно однозначное соответствие между произвольным вектором nи соответствующей ему 1-формой n ̃в виде á n ̃, vñ = n · v, то есть число пересеченных поверхностей произвольным вектором vу некоторой 1-формы n ̃равно проекции вектора vна вектор n(точка обозначает скалярное произведение).

Таким образом, дифференциальная геометрия дает исследователю надежный математический формализм, позволяющий установить взаимнооднозначное соответствие между локальным точечным описанием физических величин (импульс в данной точке в виде вектора) и нелокальным описанием (тот же импульс, но уже в объеме, окружающем эту точку в виде 1-формы). А значит, учитывая наши цели, необходимо поближе познакомиться с этим геометрическим объектом (небольшое дополнение см. в Приложении).

Нам понадобится еще одно понятие дифференциальной геометрии. Это 1-форма объема . Достаточно будет ограничиться частным случаем этого понятия для трехмерного куба в системе отсчета, относительно которой он находится в покое. Тогда 1-форма объема с 4-скоростью uи ребром L определяется как Σ = — V u= L 3 d t в случае стандартной положительной ориентации uв прошлое ( u= — d t ) или в другом варианте Σ = L 2Δ t d x . По своему геометрическому смыслу 1-форма объема представляет собой объем, «заметаемый» со временем либо за счет движения самого объема (первый вариант), либо за счет движения одной из его граней, например, площадки S yz = L 2в направлении x со скоростью u(второй вариант).

1-форма произвольного объема может быть проанализированапутем разбиения ее на введенные элементарные объемы.

Теперь мы располагаем уже всеми необходимыми понятиями, чтобы сформулировать определение [159]тензора энергии-импульса в терминах дифференциальных форм: тензором энергии-импульса называется линейный оператор с двумя входными каналами, в один из которых вводится 1-форма объема Σ, а в другой — произвольный вектор wили 1-форма σ , и в результате получается проекция 4-импульса на этот вектор или 1-форму соответственно, то есть