Айван Пастин - Теория игр в комиксах

Идея равновесия Нэша и достаточно проста, и эффективна одновременно: в ситуации равновесия каждый рациональный игрок выбирает свою оптимальную стратегию, учитывая, что другой игрок также придерживается определенной стратегии. То есть участник выбирает стратегию в зависимости от действий оппонента.

Оптимальная стратегия Rabbit films

• Если Rabbit films ожидает, что Weasel Studios выпустит фильм в октябре, то их оптимальной стратегией будет выпуск фильма в декабре, так как R:120 > R:50. Подчеркиваем R:120.

• Если Rabbit films ожидает, что Weasel Studios выпустит фильм в декабре, то их оптимальной стратегией будет выпуск фильма в декабре, так как R:90 > R:70. Подчеркиваем R:90.

Оптимальная стратегия Weasel studios

• Если Weasel Studios ожидает, что Rabbit films выпустит фильм в октябре, то их оптимальной стратегией будет выпуск фильма в декабре, так как W:10 > W:5. Подчеркиваем W:10.

• Если Weasel Studios ожидает, что Rabbit films выпустит фильм в декабре, то их оптимальной стратегией будет выпуск фильма в декабре, так как W:8 > W:7. Подчеркиваем W:8.

В ситуации равновесия обе студии выпустили бы фильмы в декабре. Это единственный исход, при котором оптимальные стратегии обеих студий позволяют достичь наилучших результатов.

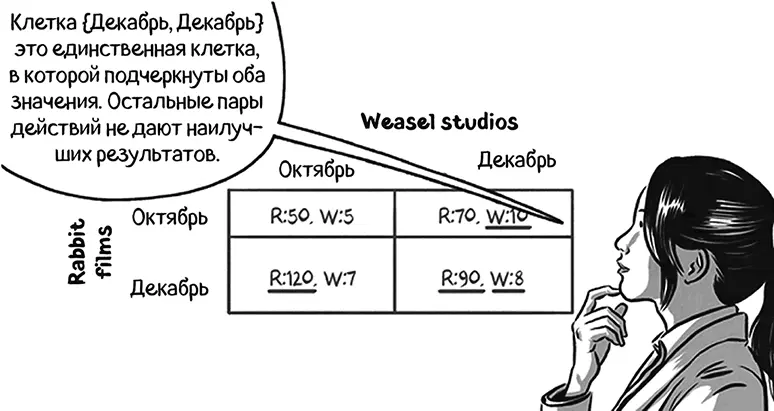
Одной из характеристик равновесия Нэша является отсутствие сожаленияу каждого из игроков. Отказ от стратегии равновесия, подразумевающей выпуск фильмов в декабре, не принес бы ни одной из студий никакой выгоды. Равновесие Нэша также является и равновесием рациональных ожиданий. В такой ситуации Rabbit films выпускает фильм в прокат в декабре, ожидая, что Weasel Studios собирается выпускать фильм в прокат в декабре. И действительно, Weasel Studios назначает релиз на декабрь. Соответственно, ожидания правильны.

«Дилемма заключенных» – это самый известный парадокс во всей теории игр. Такое название этой дилемме дал канадский математик Альберт Такер(1905–1995). Эта игра профессора Такера очень похожа на голливудскую криминальную драму, в которой каждому из двух заключенных предлагают сделку о сотрудничестве с правосудием в обмен на донос о другом заключенном. Эта дилемма наглядно показывает, как трудно может быть действовать сообща для общего блага, если люди преследуют свои личные интересы.

Стимулы, которые мы наблюдаем в «Дилемме заключенных», достаточно часто встречаются и используются учеными при анализе задач в самых разнообразных областях науки, например конкуренция компаний в экономике, общественные нормы в социологии, механизмы принятия решения в психологии, борьба животных за скудные ресурсы в биологии или борьба компьютеров за канал передачи данных.

Алан и Бен угнали машину, но их вскоре поймали. Полицейские подозревают, что до того, как их арестовали, они сбили человека и скрылись с места преступления, но у следствия нет улик, прямо указывающих на их вину. Допрос преступников ведется в разных комнатах.

И у Алана, и у Бена есть два варианта действий: они могут сохранять молчание, а могут признаться. Соответственно, существует четыре возможных исхода этой игры:

Алан сохраняет молчание, и Бен сохраняет молчание;

Алан признается, и Бен сохраняет молчание;

Алан сохраняет молчание, и Бен признается;

Алан признается, и Бен признается.

«Дилемма заключенных» может быть представлена в стратегической форме, при которой каждый ряд матрицы представлял бы возможный выбор Алана, а каждая колонка – возможный выбор Бена. На пересечениях каждого ряда и колонки мы обозначим выигрыши каждого игрока: в данном случае это будет срок заключения.

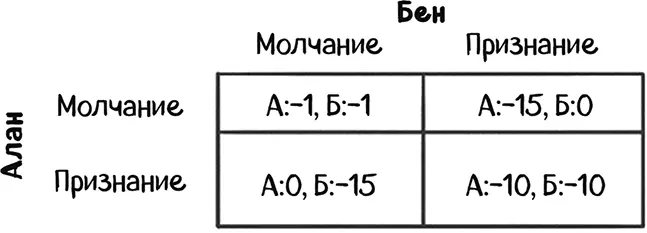
Если Алан и Бен сохранят молчание, то оба получат срок в один год за угон автомобиля. Это отрицательный расклад, поэтому их выигрыши также в минусе (Алан: –1, Бен: –1). Если оба преступника сознаются, каждый сядет в тюрьму на 10 лет (А – 10, Б – 10).

Заключенные понимают, как работает эта матрица, и знают, что имеют дело с одной и той же матрицей.

Это пример игры с одновременными ходами. Даже если заключенные не принимают решения синхронно, мы все равно можем назвать их одновременными, потому что игроки находятся в разных комнатах и ни один из них в момент принятия своего решения не знает, как будет действовать другой.

Однако заметьте, что, воспринимая эту дилемму как игру в стратегической форме, мы не говорим о возможном исходе. Мы просто обозначаем все потенциально возможные итоги, будь они разумны или нет, и записываем выигрыши, которые игроки получили бы, если бы место имел именно такой исход.

Теперь, когда мы записали нашу задачу в стратегической форме, мы можем приступить к анализу возможного результата.

Очевидно, если бы Алан и Бен вместе придумали бы свою версию произошедшего, они смогли бы сохранить молчание и попали бы в тюрьму всего на один год.

Но этот вариант не входит в систему равновесия. Для Алана стратегия «сознаться» строго доминируетнад стратегией «молчать»: всегда лучше сознаться, несмотря на его ожидания относительно действий Бена.

Точно так же и для Бена оптимальной стратегией было бы признание, вне зависимости от его ожиданий относительно действий Алана.

В ситуации равновесия Нэша в данной дилемме оба заключенных признаются. Стандартный способ записи этого исхода таков:

Это значит, что игрок, чьи выигрыши записаны в матрице в строку (Алан), сделал выбор в пользу признания, как и игрок, чьи выигрыши записаны в колонку (Бен). В равновесии оба заключенных получают по 10 лет тюремного срока.