Айван Пастин - Теория игр в комиксах

До сих пор мы рассматривали игры только с точки зрения равновесия Нэша. В тех играх равновесие Нэша делает один-единственный прогноз поведения игроков. Тем не менее люди часто сталкиваются с множеством равновесий Нэша. В играх с множеством равновесий концепция равновесия Нэша сама по себе не предоставляет нам достаточных средств для прогнозирования действий участников.

Какое же равновесие изберут участники игры с множеством равновесий?

В поисках ответа на этот вопрос американский экономист, профессор политической экономии и лауреат Нобелевской премии 2005 года Томас Шеллинг(1921–2016) пересмотрел суть экономики и ее место среди общественных наук.

Классическая игра «Битва полов» позволяет понять стимулы, возникающие в игре с множеством равновесий Нэша. Может показаться, что эта игра слишком проста и основывается на устаревших стереотипах, но она прекрасно иллюстрирует эту множественность, так как стимулы одной и той же формы проявляются в самых разных ситуациях.

За завтраком пара молодых людей, Эми и Боб, решают провести вечер вместе, но каждый из них предлагает разное занятие. Они договариваются созвониться днем и решить, куда пойти вечером.

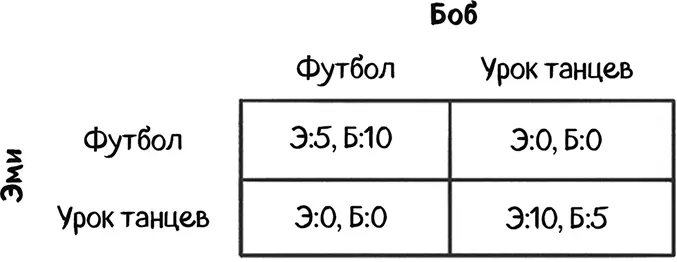
Эта матрица выигрышей иллюстрирует «счастье» участников. Числа показывают, какой исход предпочтителен для каждого игрока. Например, если Эми и Боб пойдут на футбол, выигрыш Эми составит 5. Если они вместе пойдут танцевать, Эми выиграет 10 (Э:10). Точные числа не имеют никакого значения, они лишь условно обозначают желание Эми пойти танцевать, а не смотреть футбол, так как 10>5.

Хотя Эми и Боб предпочитают по-разному проводить время, им нравится быть вместе. Они оба думают, что худшим исходом было бы провести вечер порознь. Если они в итоге выберут разные занятия, то выигрыш каждого составит 0.

В тот день на телефонной станции произошел сбой. Эми и Боб должны принять это решение, не совещаясь и не зная, что выберет другой. Так эта игра становится игрой с одновременными ходами.

В ситуации равновесия Нэша оба участника пойдут на футбольный матч.

Однако равновесие Нэша сохранится, и если они оба пойдут танцевать.

В «Битве полов» возможны два равновесия Нэша, при которых игроки с уверенностью выбирают определенный вид деятельности: «футбольное» равновесие и «танцевальное» равновесие.

Но что же Эми и Боб в итоге выберут?

Вполне вероятно, что Эми и Боб потерпят так называемую координационную неудачуиз-за несовпавших ожиданий. В этом случае ученый, занимающийся теорией игр, отметил бы «внеравновесный» исход, при котором оба участника проводят вечер порознь: ни одно из возможных равновесий Нэша не имело место.

Существуют способы преодолеть координационную неудачу в играх с множеством равновесий…

В ситуациях с множеством равновесий игроки могут координировать свои ожидания относительно одного равновесия с помощью социальных норм. К примеру, если Боб всегда старается делать все по-своему, то и Эми, и сам Боб будут ожидать, что равновесие, предпочтительное для Боба, будет доминировать в любой ситуации с множеством равновесий. В этом случае не только Боб будет рад пойти на матч с Эми, но и Эми будет рада, ведь она с Бобом, а не проводит вечер в одиночестве.

Игра «Битва полов» не предоставляет тех условий, при которых общество становится патриархальным(то есть обществом, в котором мужчины являются основными носителями власти), однако она иллюстрирует возможную выгоду доминирования по половому признаку. Возможно, это одна из причин, почему обществу так трудно перейти к более справедливой форме существования.

Если в играх с множеством равновесий отсутствует социальная норма, игроки могут воспользоваться средством координации, то есть таким коллективным наблюдением или общей историей, чтобы скоординировать ожидания относительно одного и того же равновесия.

К примеру, на радиостанции, которую слушают Эми и Боб, могут активно рекламировать их танцевальную студию. Для студии рационально вкладывать деньги в рекламу, если студия ожидает, что реклама скоординирует ожидания потребителей относительно равновесия, которое они выберут. Эми и Боб понимают, что студию рекламируют, потому что слушатели радиостанции используют рекламу, чтобы скоординировать ожидания. Соответственно, в отсутствие прямого общения между Бобом и Эми они могут использовать рекламу, услышанную в течение дня, как средство координации своих ожиданий относительно «танцевального» равновесия.

Откуда у банков столько денег? Дело в том, что банк принимает наши вклады и часть этих средств дает в кредит юридическим и физическим лицам, которые платят банку процент. Такая схема выгодна для банка, она также позволяет людям покупать недвижимость, а предприятиям – инвестировать. Но это значит и то, что все вкладчики не могут одновременно забрать свои вклады. Бо́льшая часть всех средств обычно отдана в кредит, то есть ее нельзя будет получить, пока банку не будет выплачена вся сумма.

Соответственно, даже если банк находится в прекрасном финансовом состоянии, он будет вынужден признать себя банкротом в случае бегства вкладчиков(ситуация, при которой все вкладчики одновременно пытаются изъять свои вклады).