Айван Пастин - Теория игр в комиксах

Если Radish продолжит работать, он понесет убытки, равные –50, при условии, что Kalemart также продолжает работать, что произойдет с вероятностью k. Radish получит 100, если Kalemart «вылетит», что произойдет с вероятностью (1 – k). Таким образом, для Radish:

«Рэдишу» безразлично, продолжать работу или закрываться, только если его ожидаемая прибыль от этих альтернатив равна:

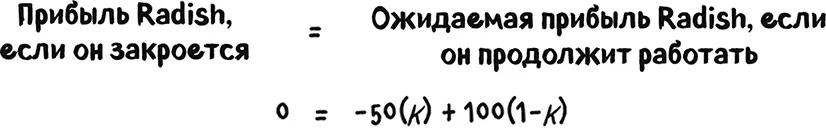
Чтобы найти равновесную вероятность того, что Kalemart продолжит работать, разрешим эту задачу относительно k и получим, что k= ⅔.

Равновесная вероятность того, что Radish продолжит работать, равно ⅘. Это можно рассчитать, пытаясь найти такую вероятность, с которой Kalemart будет безразлично – работать или закрываться.

Если Kalemart продолжает работать, он понесет убытки в размере –20, при условии, что Radish работает, что произойдет с вероятностью ⅘. Kalemart получит прибыль в размере 80, если Radish «вылетит», что произойдет с вероятностью ⅕. Для Kalemart в равновесной ситуации ожидаемая прибыль от прекращения работы (равная нулю) равна ожидаемой прибыли от работы.

В равновесной ситуации Kalemart продолжил бы работу с вероятностью ⅔, а Radish остался бы с вероятностью ⅘, поэтому мы можем рассчитать вероятность каждого возможного исхода.

Вероятность того, что оба магазина закроются, равна 1/15, то есть мы умножаем вероятность того, что Kalemart закроется, на вероятность прекращения работы Radish: (1/3)*(1/5)=1/15.

Вероятность того, что оба магазина продолжат работу, равна 8/15, то есть мы умножаем вероятность того, что Kalemart продолжит работать, на вероятность работы Radish: (2/3)*(4/5)=8/15. В этом случае оба магазина несут убытки. Этот исход похож на один из возможных исходов в «Кто первый струсит», где оба подростка демонстрируют свою смелость и погибают в аварии.

Вероятность того, что Kalemart в конце концов останется единственным магазином в городе, или того, что Radish создаст продуктовую монополию, можно рассчитать этим же способом.

Также возможно смоделировать другую версию «Игры навылет», в которой оба игрока продолжают работать, у них есть возможность закрыть магазин попозже. В этом случае их конфликт продлится еще дольше, а их убытки будут расти. Это явление известно под названием война на истощение. Этот термин был заимствован из военного лексикона. В подобных играх могут происходить затяжные, изматывающие конфликты, даже если выигрыш на самом деле совсем незначителен по сравнению со всеми потерями и убытками.

Из всех тем в теории игр равновесие Нэша в смешанных стратегиях, наверное, вызывает наибольшие разногласия. Сторонники смешанных стратегий подчеркивают, что многие игры, например «Камень, ножницы, бумага» или «Валютная спекуляция», не имеют равновесия Нэша в чистых стратегиях, но в них наблюдается очень интересное равновесие Нэша в смешанных стратегиях. Они также утверждают, что даже в таких играх, как «Кто первый струсит» или «Игра навылет», в которых есть равновесие Нэша в чистых стратегиях, это равновесие зачастую является полностью интуитивным, так как оно выявляет неуверенность игроков.

Тем не менее оппоненты смешанных стратегий заявляют, что случайный выбор не является разумным человеческим поведением. Неужели люди принимают решения наугад? И в связи с тем, что при равновесии участники индифферентны, что мотивирует их выбирать как раз те вероятности, которые подталкивают других игроков к индифферентности?

Одним из защитников смешанных стратегий был американо-венгерский экономист Янош Харсаньи(1920–2000), который ввел понятие « очищение». В 1994 году он разделил Нобелевскую премию по экономике с Джоном Нэшем и немецким экономистом Рейнхардом Зельтеном(род. в 1930 г.).

Янош Харсаньи утверждал, что даже если игроки выбирают чистые стратегии, если присутствует даже малейшее сомнение в выигрышах друг друга, со стороны будет казаться, что они делают случайные выборы.

Знаменитое «очищение» Яноша Харсаньи доказывает, что если игроки почти, но не полностью уверены в выигрышах других участников, то отдельному игроку может показаться, что вероятность выбора другим игроком определенной линии поведения точно равна той вероятности, с которой мы имеем дело в равновесиях Нэша в смешанных стратегиях без неуверенности о чужих выигрышах.

Это значит, что равновесие Нэша в смешанных стратегиях относительно, даже если вы не верите, что людям свойственно принимать решения наугад.

Одним из примеров равновесия Нэша в смешанных стратегиях являются игроки, которые случайным образом выбирают свои возможные действия. Еще одним примером можно назвать некоторую неуверенность о выигрышах других игроков. Игра под названием «Уклонение от уплаты налогов», в которой взаимодействуют налогоплательщики и налоговая служба, может служить третьим примером.

Представьте ситуацию: женщина, владелица предприятия, должна заполнить налоговую декларацию. Для простоты допустим, что у нее есть два варианта: действовать согласно букве закона или уклоняться от уплаты налогов. Предположим, что с нравственной точки зрения уклонение от уплаты налогов нормально.

Налоговая служба, естественно, может поймать «уклониста», но аудит – это дорогостоящая процедура. Однако в аудите нет нужды, если налогоплательщик не уклоняется от уплаты налогов.

В этой игре нет равновесия Нэша в чистых стратегиях.

Налогоплательщик, несомненно, будет действовать в рамках закона, если точно знает, что его будут проверять. Тут не может быть равновесия Нэша: если налогоплательщик точно будет уплачивать налоги, государству нет нужды проводить аудит.