В Конелес - Сошедшие с небес и сотворившие людей
- Название:Сошедшие с небес и сотворившие людей
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2000
- Город:Вече
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
В Конелес - Сошедшие с небес и сотворившие людей краткое содержание
В своей книге В. Ю. Конелес — геофизик, астроном-любитель, переводчик, региональный эксперт Ассоциации "Экология непознанного" (Москва), член "Международного общества по исследованию НЛО" ("International Society for UFO Research" (ISUR), Atlanta, Georgia, USA) — обращается к самым загадочным страницам древнейшей летописи человечества. Используя огромный исторический материал, автор приходит к выводу о существовании на Земле в прошлом (не позднее XV—X тысячелетий до н. э.) необычайно высокоразвитой цивилизации, владевшей глубокими научными знаниями и активно использовавшей неизвестные нам технологии.
Особое внимание автор уделяет Шумерской цивилизации — одной из самых передовых цивилизаций древности, а также самым различным свидетельствам того, какую роль сыграли в истории человечества "сошедшие с небес".
Сошедшие с небес и сотворившие людей - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В тексте АО.6478 приводится список 26 звезд так называемого "тропика Рака" и указаны расстояния между ними. При этом величина расстояний представлена в виде угла небесной дуги, ее временного эквивалента (beru — "беру") и некоего хронометрического механизма, использующего принцип водяных часов.
Ф. Тюро-Дэнгин показал, что в абсолютных значениях "небесный беру", вероятно, составлял 10 692 м [442].
Современный западный календарь восходит к ниппурскому календарю. Специальные исследования установили, что этот календарь был основан в начале IV тысячелетия до н. э., и пришел он именно из Шумера. Профессор Стивен Лэнгдон продемонстрировал, что по положению Солнца относительно определенных небесных тел можно определить точный момент наступления Нового года. По его данным, ниппурская система времяисчисления была создана в 4400 году до н. э. [399]. Он же доказал, что шумеры хорошо знали о явлении прецессии земной оси еще в 6510 году до н. э.
К этому же выводу пришли профессора В. Хантер, А. Джеремаяс и X. Хилпрехт. Причем, изучив хранящуюся в музее Берлина табличку под каталоговым номером VAT.7847, Джеремаяс заключил, что исходная "точка отсчета" у шумеров находилась примерно в XI тысячелетия до н. э. Точка весеннего равноденствия находилась тогда в со тзвездии Льва (точнее, в интервале 10 860—8700 годов до н. э.; заметим, что это совпадает с непосредственно послепотопным периодом!).
Согласно календарю иудеев, сейчас идет 5759 год; по православному календарю — 5510, а по католическому — 4006 год. Вообще, многие теологи пытались вычислить дату начала на основе сведений, излагаемых в Книге Бытия. В настоящее время существует около 200 вариантов расчета времени начала мира, которые в основном лежат в интервале 3483—6984 годы до н. э. [86]. Но установлено, что иудейский календарь основан на ниппурском календаре, введенном в 3760 году до н. э. И существуют указания на то, что в том году Землю посетил AN (или An и на аккадском) — правитель Нибиру [120] Эта дата может и не совпадать с периодом сближения Нибиру с Солнцем.
. Это имя означает "Небесный", но само слово AN стало составной частью многих астрономических терминов (AN-UR — "небесный горизонт"; AN-PA— "точка зенита"; NIN-ANNTJ — первый месяц года; AN-BIL — "широта, соответствующая солнцестоянию" и т. д.) [435, с. 187]. Оно же было составной частью слова Anunaki. Древнекитайские слоги также выдают их шумерские корни (в частности, "kuan" — "храм, одновременно служащий обсерваторией"; на шумерском "KU-AN" означает "проход в небеса"; опять же, традиция совмещения функций храма и обсерваторий восходит к шумерским и вавилонским зиккуратам) [434, с. 209]. Слово "год" в европейских языках (annum — на латыни, аппее — на французском, annual — на английском) также восходит к тому времени, когда Землю посетил Ану.
По другой версии, в это время рядом с Солнечной системой прошла звездная система Сириуса [80]. Во всяком случае, по мнению ряда исследователей, некий таинственный персонаж мифологии африканского племени догонов — Бледный Лис, "спустился в ковчеге со звезды По (Сириуса)" и передал аборигенам такие сведения о Солнечной системе и звездах системы Сириуса, что это позволило выдвинуть и обосновать версию о его действительно внеземном происхождении [107, с. 76—86; 78; 99].) Звезды этой группы входят в десятку ближайших к нам — "всего" 2,7 парсека. Однако у этой версии есть немало серьезных оппонентов.
Математика. До 1920 года было принято считать, что наука о числах родилась в Древней Греции. Однако выяснилось, что почти все свои знания в этой области греки почерпнули в Двуречье и Египте. Пришедшая к нам от греков шестидесятеричная система исчисления утвердилась в Греции во времена Гиппарха (190— 120 годы до н. э.) и за считанные десятилетия получила широкое распространение. В частности, греки заимствовали вавилонский способ вычисления квадратных корней и соотношения сторон прямоугольного треугольника. Известная каждому школьнику теорема Пифагора на самом деле была известна в Двуречье, по крайней мере, в XVIII веке до н. э. Согласно "Британнике", на Ближнем Востоке и в Европе каменного века эту теорему знали за 1500— 2000 лет до рождения Пифагора.
Шумерская система исчисления называется шестидесятерич-ной. Система чисел базировалась на комбинации 6 и 10.
Таблица 8
| Десятеричная | Шестидесятеричная |
| 1 | 1 |
| 10 | 10 |
| 10x10 | 10x6 |
| (10х10)х10 (10х10х10)х10 | (10х6)х10 (10х6х10)х6 |
Счет шел до шестидесяти. 120 равнялось двум gesh". Половина "геш", соответственно, составляла 30. С точки зрения математики такая система намного "выгоднее" десятеричной. 10 делится только на 2 и 5. 100 делится на 2, 4, 5, 10, 20, 25 и 50. Но 60 делится на 2, 3, 4, 5, 6, 10, 12, 15, 20 и 30, а если возвести 60 во вторую степень — то еще на 9, 16 и другие числа [136, с. 82]. Внешне запись цифр выглядела своеобразно (рис. 145).
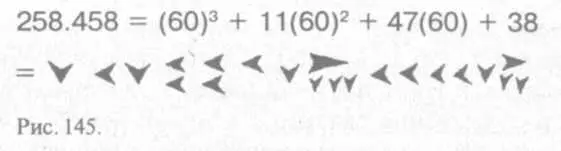
Мы унаследовали от шумеров 12 в счете месяцев и часов дня, 60 — в счете минут и секунд (времени и дуги). 360 (60x60) градусов — круг в геометрии и сумма углов четырехугольника. 180 градусов — сумма углов треугольника. В теоретической и прикладной геометрии это позволяло ученым древнего Двуречья рассчитывать площади сложных фигур. Шумеры знали и применяли правила сложения, вычитания, умножения и деления. Были найдены математические таблицы, напоминающие таблицы Брадиса, содержащие значения квадратичных и кубических значений чисел, таблицы умножения и деления, экспоненциальные функции для вычисления сложных процентов [176, с. 247].
Арифметические, геометрические и алгебраические задачи, ставящие в тупик нынешних студентов, решались шумерами совершенно верно. Ф. Тюро-Дэнгин в работе "Вавилонские математические тексты" [443] показал, что шумеры использовали извлечение корней и возведение в степень и решали уравнения с двумя и тремя неизвестными. Счетоводы со скрупулезной точностью вели учет продукции, рабочей силы и т. д.
Отметим еще два существенных момента. Шумеры первыми ввели и определили то, что одни и те же цифры в цифровой группе имеют разное числовое значение. Так, в числе 777 последняя цифра означает саму себя, стоящая перед ней — уже в 10 раз большую, и т. д. Также первыми шумеры ввели и значок, обозначающий "ничто", "нет" или нуль, скорее всего из утилитарных соображений — чтобы избежать ошибок при написании крупных чисел, но важно, что это было в полном смысле то, что мы называем сегодня нулем [136, с. 83-84].
Главным числом, означаемым большим кругом, было уже упоминавшееся ранее SAR или (Shar на аккадском) — 3600 — "царское число" лет, за которое Нибиру делает один оборот вокруг Солнца. Среди тысяч математических табличек многие содержали "астрономические числа". Таким было, например, 195 955 200 000 000 — пятнадцатизначное число на табличке, обнаруженной при раскопках бывшей Ниневии близ Куюнджика. (Для сравнения: греки в пору расцвета их цивилизации не знали чисел больше 10 000 и все величины, превосходящие эту, попросту обозначали — "бесконечно".)
Читать дальшеИнтервал:
Закладка:









