Александр Александров - Цифровые методы анализа будущего

© Александров А. Ф., наследники, 2015

© ООО Группа Компаний «РИПОЛ классик», 2015

Предположим, что все объекты мироздания (в том числе процессы, происходящие в них) соответствуют некой идеальной эллиптической модели (научной гипотезе, основанной на компромиссе различных мнений), дающей полное представление о данном объекте (процессе) мироздания.

Данное утверждение, если оно нами принимается, неизбежно приводит нас к другой, еще более интересной мысли.

Цель любого научного поиска – построить эллиптическую модель конкретного объекта или процесса, которая максимально точно совпадала бы с идеальной эллиптической моделью данного объекта (процесса).

Таким образом, любой человек, высказывая свое суждение о любом объекте (процессе) мира, должен стремиться к тому, чтобы это представление (эллиптическая модель) об этом объекте (процессе) было максимально близким к истинному содержанию (к идеальной эллиптической модели) данного объекта или процесса.

Для полной ясности рассмотрим несколько рисунков, которые помогут нам выделить несколько вариантов объектов мира, отличных от эллипса, но основанных на эллиптической модели, которые мы можем наблюдать и изучать. Весь этот философский туман скоро рассеется, когда от слов мы перейдем к зарисовкам. Как гласит народная мудрость, лучше один раз увидеть, чем сто раз услышать.

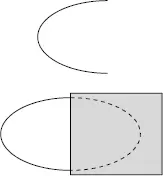
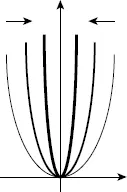
Парабола

Вариант эллипса, часть которого недоступна для наблюдения (скрыта).

Гипербола

Вариант эллипса, наложенного на сферу, при условии, что длина большой оси эллипса меньше, чем длина окружности экватора (или большого круга сферы), но больше диаметра самой сферы.

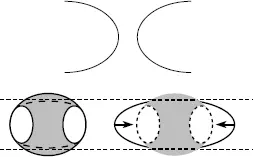
Края эллипса загибаются на сферу, образуя линии, очень похожие на гиперболу.

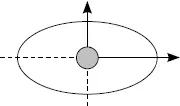
Точка и мнимые прямые

Рассмотрим эллипс, в центр которого поместим создателя данной эллиптической модели. Как мы знаем, любой эллипс имеет большую и малую оси (или два диаметра), которые перпендикулярны друг другу (угол между ними равен 90°). Нетрудно предположить, что в центр данного эллипса можно было бы поместить точку начала координатных осей, проходящих через большую и малую оси эллипса.

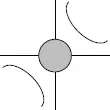
Точка и действительные прямые

Если мы зададим систему координат, в центр которой поместим наблюдателя, то оси координат будут асимптотами [1] Асимптотой называется прямая, к которой линия стремится приблизиться, но никогда её не достигает (не касается). для любых гипербол, заданных стандартным уравнением гиперболы (y=1/xn – обратная степенная функция); не будем забывать, что сами гиперболы были нами получены (имеются в виду схожие с гиперболой линии) из эллипса.

Две параллельные прямые.

Если мы рассмотрим четную (делится на 2) степенную функцию, которая имеет следующую общую формулу: у = kx 2n+ b, то ее графиками будут параболы, которые с увеличением показателя степени своими ветвями все более и более приблизятся к вертикальной оси координат, стремясь превратиться в две полупрямые, параллельные вертикальной оси.

Если мы сравним общее уравнение, задающее параболы, с общим уравнением прямых линий, то увидим их внешнее сходство.

Y = kx 2n+ b– уравнение парабол, у = kx + b– уравнение прямых.

Если мы вспомним известную из школьного курса алгебры формулу «разницы квадратов»: а 2– b 2= (a-b)(a+b)– и применим ее в приложении к некоторым уравнениям парабол: у = х 2+ b 2, то мы увидим связь между параболами и прямыми: у = х 2+ b 2= (x-b)(x+b). Как вы сами можете видеть, в данной формуле имеется уравнение параболы у = х 2+ b 2и уравнения прямых у = х – bи у = х + b, которые указывают на тот факт, что при вырождении параболы переходят в параллельные или совпадающие прямые (как мы это видели, говоря о повышении степени в уравнении парабол).

Мы рассмотрели все возможные случаи, которые могут быть получены на основе эллипса. Включая сам эллипс, мы получили шесть возможных вариантов, которые позволят нам рассмотреть шесть различных моделей объектов и субъектов (наблюдателей) мира, которые будут создавать гармоничные пары «объект – субъект», которые помогут нам понять возможные варианты отношений человека с окружающим миром.

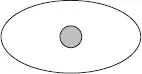
Модель «эллипс»

Особенности объекта.Доступен для изучения; имеется возможность определить основные параметры; известна или понятна конечная цель исследования объекта (процесса, теории и т. д.).

Особенности субъекта.Он создатель своего мира, в котором все ясно и понятно, в котором только «свои», все те, кто его понимают и принимают его мир. Он конструктор, изобретатель, автор совершенной, логической модели, которая, по его убеждению, максимально совпадает с идеальной эллиптической моделью объекта исследования.

Модель «парабола»

Особенности объекта.Фактически неизвестен; имеются отдельные фрагменты, неясные очертания, какие-то общие и весьма расплывчатые сведения о нем; неизвестны основные параметры; совершенно не определена цель исследования объекта, в отдельных случаях, отсутствует интерес к объекту как к возможной цели для исследования;

Особенности субъекта.Это исследователь, теоретик, философ, мыслитель, способный интуитивно выделять неизвестные на данный момент объекты (темы исследований), которые в ближайшем или далеком будущем будут весьма важны и перспективны; он способен выделить отдельные важные параметры нового объекта, определить направление исследования и составить прогноз на возможные результаты исследования;

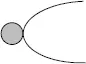
Модель «гипербола»

Особенности объекта.Объект известен, полностью изучен, готов к применению или копированию (тиражированию, повторению).