Марсело Санчес - Эмбрионы в глубинах времени

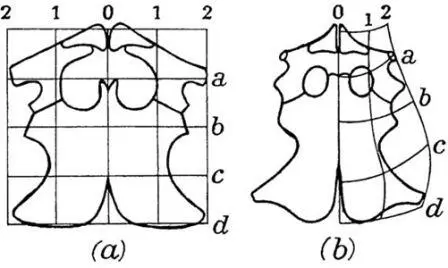
Геометрический подход Томпсона заслужил много внимания и похвал, и повлиял на другие области знаний. [57] Книга Томпсона «О росте и форме» оказала сильное влияние на работу Клод Леви-Стросс по поддержке идеи трансформации — одного из принципов структурализма в антропологии (Wilcken 2010). Но его широкое применение надолго задержалось. Методом стали интенсивно пользоваться лишь в последние десятилетия, когда были разработаны подходящие алгоритмы для работы с комплексной информацией геометрического плана. Начиная с 1980-х годов пережила свой расцвет дисциплина геометрической морфометрии, и были разработаны изощрённые методы работы и компьютерные программы, позволяющие сравнивать разные виды и прослеживать изменения, происходящие в процессе роста; в случае позвоночных большинство из них касалось их черепов. При геометрическом подходе фиксируется много точек-ориентиров и проводится количественная оценка того, как весь их массив различается от вида к виду или между стадиями в серии образцов, иллюстрирующих рост. Существуют различные подходы, основанные на использовании точек-ориентиров; у каждого из них своя собственная математическая структура и они включают методы, основанные на измерении деформации, суперпозиции и линейных расстояний. [58] Чтобы получить начальное представление о морфометрических методах и их использовании в палеонтологии, см. прекрасную серию публикаций Норма МакЛеода в Палеонтологическом информационном бюллетене Палеонтологической Ассоциации: www.palass.org/modules.php?name=palaeo_math.

Альтернативный и более простой математический подход по сравнению с геометрическим подходом Томпсона был разработан примерно в то же самое время. Этот подход также оказал значительное влияние на исследования роста. В 1936 году Джулиан Хаксли и Жорж Тессье опубликовали одновременно на английском и французском языках работу, которая ввела в оборот простое, но изящное уравнение, которое суммирует отношение между двумя измеряемыми величинами. Это отношение было выражено как

y = x a

или в логарифмической форме,

log y = a log x,

где a — величина, вычисляемая с помощью отношения.

Математический график роста, или онтогенетическая траектория, после логарифмического преобразования обычно представляется в виде прямой линии. Направление или наклон и положение или пересечение с вертикальной осью графика — переменные величины, которые нужно вычислять.

Параметры, которые относятся к исследованию роста — это скорость, продолжительность, начало и завершение. Эволюция включает прерывание, изменения и перестановки этих параметров. Рост может порождать изменение формы, и это вызвано изменениями размеров, которые не находятся в отношении 1:1 с формой. Если отношение размеров к форме постоянно, мы имеем дело с изометрией. Это довольно редкий случай, поскольку мы гораздо чаще сталкиваемся с изменением формы, зависящим от изменения размеров, или аллометрией; этот термин Хаксли и Тессье использовали в своей статье 1936 года. [59] Гейон (2000) подробно обсуждал историю концепции аллометрии и нескольких предшественников Хаксли и Тессье в этом плане. Из-за аллометрических отношений пропорций в процессе роста особи одного и того же вида могут иметь различную форму тела на разных стадиях роста. Из этого также следует, что внешний облик видов может меняться, если они обладают различными видами аллометрических отношений в процессе роста, или же если в процессе роста имеет место один и тот же вид отношений, но рост тормозится, или, напротив, продолжается дольше. В онтогенетическом шкалировании различия между двумя видами могут быть целиком отнесены к различиям в размерах, если они попадают на одну общую для обоих видов траекторию роста. Здесь различия являются следствием продления времени роста, или же его остановки. И наоборот, можно сделать вывод об изменениях в характере роста, если изменчивость не вписывается в одну общую траекторию.

У математического подхода, разработанного Хаксли и Тессье, было несколько предшественников в конце девятнадцатого века, но лишь в двадцатом веке появилось сообщество биологов, готовых освоить и использовать новый числовой инструмент. [60] Значительным шагом вперёд было многомерное обобщение аллометрии, осуществлённое Жоликуром (1963). Сразу же после публикации уравнения роста, которое изящно выражало отношение между двумя размерными величинами, в этом ключе была исследована эволюция вымерших видов. Аллометрический подход был с энтузиазмом принят сообществом палеонтологов, и результатом этого стали многочисленные исследования эволюционных рядов тех таксонов, у которых приобретение какой-то специфической особенности выглядело результатом аллометрического роста — например, рога у ореодонтов (вымерших родственников верблюда), длина ростральной области у лошадей с эоцена до наших дней, гребень на голове у позднемелового динозавра Protoceratops и удлинённые верхние остистые отростки позвонков, образующие «парус» у пеликозавров, очень дальних, ранних родственников млекопитающих из позднего карбона и ранней перми Техаса. По итогам тех исследований было объявлено, что этими особенностями управляют простые взаимосвязи и прямые и постоянные аллометрические соотношения. Проведённые позже ревизии многих из этих исследований показали иное. Когда было обнаружено больше ископаемых остатков и были построены надёжно документированные эволюционные древа для этих групп организмов, стало понятно, что сама аллометрия также эволюционирует, что организмы представляли собой мозаику особенностей строения, растущих с различной скоростью, и что эти изменения находились под управлением экологических факторов.