Максим Франк-Каменецкий - Самая главная молекула. От структуры ДНК к биомедицине XXI века

Попробуйте-ка теперь распутать! Каждому ясно, чем фигура (5) отличается от фигуры (3): их никаким образом нельзя перевести одну в другую, не порвав цепь. Узел (5) называют трилистником или клеверным листом, так как его можно переделать вот так:

Думаю, теперь вы согласитесь, что понятие узла имеет строгий смысл только для замкнутых цепей, хотя в домашнем обиходе вы можете продолжать называть узлами фигуры типа (1), если вам это очень нравится.

Итак, мы уже знаем два узла – тривиальный (среди узлов он занимает то же положение, что и нуль среди чисел) и трилистник, (5) или (6). Следующий после трилистника по сложности узел называется восьмеркой. Он выглядит так:

А это что такое?

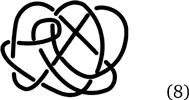
Представьте себе, что такая штука сделана из веревки. Можно ли, не разрывая веревку, перевести ее в простое кольцо (тривиальный узел), или в трилистник, или в восьмерку? Или нельзя? Иными словами, до какого простейшего вида этот узел можно распутать?

Первым всерьез заинтересовался узлами британский физик и математик П. Тэйт. Это было в 1860-х годах. Тогда физики (как, впрочем, и сейчас) хотели понять, как устроены простейшие частицы материи. Тогда, как и сейчас, они думали, что частицы могут представлять собой вихри электричества. Как-то в письме к Тэйту Максвелл написал: «А что, если этот вихрь будет заузлен?» И нарисовал трилистник.

Тэйт имел склонность к абстрактным математическим построениям. Он стал думать: какие еще бывают узлы? Но вскоре совсем забыл о частицах (будто знал, что с ними и через полтораста лет не разберутся) и стал просиживать долгие часы с веревкой, завязывая всевозможные узлы. Тэйт составил первую таблицу узлов. В ней он последовательно разместил те узлы, которые смог придумать. В дальнейшем была проведена полная «инвентаризация» всех узлов, имеющих менее десяти пересечений на их проекциях. Таких узлов набралось 84. Часть из них изображена на рис. 35.

Узлы располагают по возрастанию минимального числа пересечений на их проекции. Для трилистника это число равно трем, для восьмерки – четырем. Если есть несколько разных узлов с одинаковым числом пересечений, то они группируются в таблице вместе и каждый получает, кроме обозначения числа пересечений, еще и дополнительный индекс.

Тэйт заинтересовал проблемой узлов знакомых математиков. Повозившись с узлами лет 60, они довольно здорово наловчились распутывать сложные узлы и в 1928 году придумали инвариант узла.

Инвариант узла – это такое алгебраическое выражение, значение которого не меняется, как бы вы ни запутывали узел. Умение вычислять инвариант позволяет в принципе распутать любой узел. Достаточно определить инвариант, а затем сравнить его со значениями инвариантов, вычисленными для узлов, вошедших в таблицу. Наиболее удобным инвариантом оказались так называемые полиномы (многочлены) Александера ∆( t ). Для тривиального узла ∆( t ) = 1. Для трилистника ∆( t ) = t 2 —t + 1. Для восьмерки ∆( t ) = t 2–3 t + 1 и т. д. Таким образом, каждый узел характеризуется не отдельным числом, а целым алгебраическим выражением, в котором есть некая переменная, не имеющая специального смысла.

Если вы умеете вычислять полином Александера, то довольно быстро убедитесь, что фигура 7 – это на самом деле тривиальный узел, только сильно запутанный. Возможно, вы этого делать не умеете, и придется повозиться, чтобы в этом убедиться. Или вы должны будете мне просто поверить.

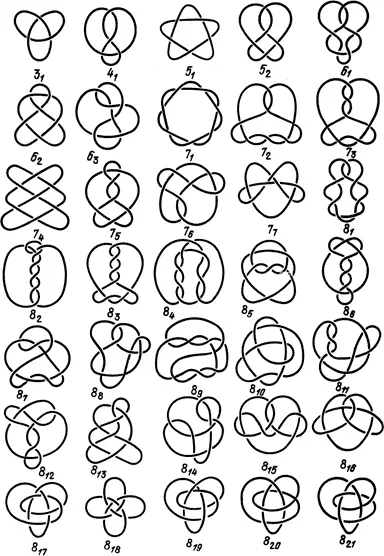
Рис. 35.Узлы

«Все это, конечно, очень мило, – скажете вы. – И даже довольно занимательно. Но какое это имеет отношение к молекуле ДНК?» Прошу прощения, я действительно немного увлекся.

Идею завязать какую-нибудь молекулу в узел стали всерьез обсуждать в начале 1960-х годов. Наверное, раньше об этом тоже говорили, но в шутку. Просто к указанному времени появились люди, для которых это перестало казаться смешным. Речь идет, разумеется, об истинном узле – трилистнике, восьмерке или более сложном. То, что молекулы могут образовать тривиальные узлы, т. е. быть замкнутыми, известно со времен Фридриха Кекуле. Но попробуйте завязать бензол в узел. Ясно, что это невозможно – его кольцо имеет слишком маленькую дырку. Да и потом, как его завяжешь? Ведь молекулу не возьмешь руками за концы, как кусок веревки. Можно поступить иначе. Сделать концы молекул «липкими». Тогда можно надеяться, что при случайном сближении концов в молекуле возникнет узел.

Для того чтобы молекула завязывалась в узел, она должна быть достаточно длинной. Но какой все-таки должна быть ее длина? Так возникает вопрос, на который непросто ответить и который в более общем виде формулируется следующим образом: какова вероятность того, что при замыкании цепи, состоящей из п сегментов, возникнет нетривиальный узел?

Речь идет о сегментах, а не об атомах и даже не о мономерных звеньях, потому что разумно говорить о некоторой идеализированной цепи, в которой под сегментом понимается более или менее прямолинейный отрезок. В жестких полимерных цепях в этот отрезок входит очень много атомов и даже много мономерных звеньев. Так называемая свободно-сочлененная цепь, с помощью которой теоретики моделируют реальные полимерные молекулы (хотя эта модель, как и всякая модель вообще, имеет ограниченную область применения, в чем читатель сможет еще убедиться), выглядит примерно так:

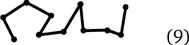
Узнаете? Да это же траектория движения абсолютно пьяного человека, о котором шла речь в главе 3. Я нарисовал плоский аналог незамкнутой полимерной цепи из 10 сегментов. Кружочки между сегментами означают шарниры. Представьте теперь, что вы заставляете эту цепь случайно замыкаться в трехмерном пространстве. (На плоскости, разумеется, вообще никаких узлов быть не может. Интересно, что в четырехмерном пространстве узлов тоже не бывает. Они возникают только в пространстве трех измерений.) Итак, свободно-сочлененная цепь случайно замыкается. Это происходит много раз. Сколько же получится при этом нетривиальных узлов? Их доля и будет мерой вероятности образования узлов. Но не пытайтесь угадать эту вероятность. Вам это не удастся! Интуиция здесь не поможет. Более 40 лет назад этот вопрос превратился в навязчивую идею у меня и у моих товарищей по работе – Вадима Аншелевича, Александра Вологодского и Александра Лукашина. Мы тогда еще ничего не знали ни о Тэйте с его таблицей узлов, ни о существовании полиномов Александера.