Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

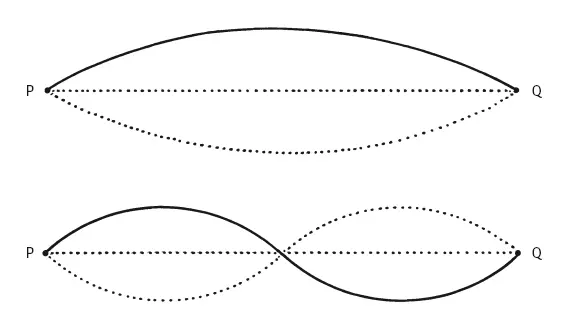
Струны, колеблющиеся в соотношении 2:i. Их колебания сходятся в одной точке (то есть приходят к согласию) после каждой второй пульсации (то есть отступления от оси) более короткой струны

Теория Бенедетти выглядела так: поскольку октава образуется из соотношения двух колеблющихся струн 2:1, каждое второе колебание, производимое более высокой струной, будет совпадать с колебанием, производимым более низкой струной. Когда пропорции, образующие различные созвучия, усложняются, это приводит к тому, что подобное совпадение колебаний происходит все реже и реже – поэтому они звучат менее консонантно. А значит, несмотря на утверждения Пифагора и Царлино, не существует единого набора гармоничных соотношений: диссонансы возникают нерегулярно.

Галилео Галилей развил эту мысль. Возьмем две струны, колеблющиеся в соотношении 3:2, объяснял он. Их пульсация начнется одновременно, затем произойдет колебание верхней струны, дальше нижней, потом опять верхней, и, наконец, цикл замкнется очередным одновременным колебанием обеих струн (этот ритмический рисунок легко изобразить, постукивая по столешнице двумя руками – одной в трехдольном ритме, другой в двудольном). По мере усложнения музыкальных интервалов рисунок будет становиться все более хаотичным, а звучание – неприятным, подвергающим “барабанную перепонку постоянной пытке, сгибающим ее одновременно в противоположных направлениях, посылающим ей противоположные сигналы”, другими словами – диссонантным.

В соответствии с семейной традицией Галилеев эстетические приципы, которые Галилео вывел из своей теории, были использованы для того, чтобы вбить еще один кол в и без того не слишком устойчивое здание системы Царлино. Октава, провозгласил он, вовсе не является чудесным созвучием – напротив, это очень пресное сочетание нот, поскольку ритмический рисунок 2:1 чрезвычайно скучен. То ли дело квинта, которая во всей своей сложности дает на выходе интересную комбинацию “сладости и остроты”!

Так или иначе, и эта теория консонанса не обошлась без существенных изъянов. Если принять ее за основу, то получится, что две струны будут звучать гармонично, только если их вибрации начинаются в одно и то же мгновение – ведь иначе их чередующиеся колебания никогда не сойдутся в одной точке! Но практика показывает, что это вовсе не так (и именно поэтому Ньютон с ходу отверг теорию Галилея). Есть и еще одна неувязка: пульсации струн, образующие сложное соотношение квинты в равномерно-темперированном строе, не сойдутся вновь, даже будучи изначально “запущены” одновременно. При этом равномерная квинта, разумеется, звучит более стройно, чем, скажем, полутон (например, сочетание нот ми и фа), в котором вибрации двух струн сходятся воедино на каждом пятнадцатом колебании. Словом, эта гипотеза была попросту неверна.

Впрочем, наготове уже была альтернативная теория, авторства Кеплера, чьи три закона движения планет навсегда изменили наше представление о Солнечной системе. В его модели гармонической вселенной наука, математика, музыка и религиозные доктрины объединились в фантастическое, захватывающее дух оправдание тезисов Царлино.

Математические закономерности в природе – особенно в небесах – занимали Кеплера с раннего детства. Его зрение поразила оспа, но в воображении ему все равно являлись чудесные картины: “небосвод, весь выложен кружками золотыми” [31] Здесь и далее перевод с английского Т. Щепкиной-Куперник. , как сформулировал это Шекспир в “Венецианском купце”. Он верил, что наука поможет ему доказать достоверность поэтичного шекспировского описания этого горнего пейзажа: “И самый малый, если посмотреть, поет в своем движенье, точно ангел… ”

“Гармония подобная живет, – продолжал поэт, – в бессмертных душах, но пока она земною, грязной оболочкой праха прикрыта грубо, мы ее не слышим”. Кеплер мечтал записать музыку сфер – желание, которое у него появилось еще в школе в Тюбингене, где Михаэль Местлин, преподаватель птолемеевской астрономии, тайком познакомил его с теорией Коперника. От Местлина он перенял коперниковскую точку зрения, согласно которой Солнце располагается в центре Вселенной и, “словно бы сидя на королевском троне, правит семьей планет, вращающихся вокруг него”. И все же многие вопросы оставались открытыми. Почему планет всего шесть – а не двадцать и не сто? Почему размер Солнца, плывущего над горизонтом, составляет 1/720 описываемого им круга? И с какой целью зодиак делит небо на двенадцать частей? Ответы на эти вопросы порой дарил случай.

Впервые так произошло в июле 1595 года, когда Кеплер преподавал ученикам геометрию. Он нарисовал на доске фигуру: вписанный в круг треугольник, внутрь которого, в свою очередь, вписан еще один круг, – и вдруг его осенило, что соотношение двух этих кругов тождественно соотношению орбит Сатурна и Юпитера. Что если попробовать передать расстояния между Юпитером и Марсом, Марсом и Землей и так далее с помощью других геометрических фигур? Используя пять Платоновых тел – трехмерных фигур, все грани которых идеально симметричны, – он убедился, что пасьянс сходится (набор этих тел описан Евклидом: пирамида, куб, восьмигранник-октаэдр, додекаэдр, состоящий из двенадцати пятиугольников, и икосаэдр, состоящий из двадцати равносторонних треугольников). Удивительно, но каждая из этих фигур в самом деле идеально заполняла промежутки между вращающимися небесными телами. Это открытие стало первым шагом в процессе, который Кеплер называл своим восхождением “по гармонической лестнице небесных движений… туда, где скрывается первопричина всех вещей”. Теперь он был уверен, что в основе божественного замысла лежит геометрия. А поискав еще немного, он нащупал формулы музыкальных консонансов в пропорциях, которые образуют правильные многоугольники, вписанные в круг.

К сожалению, положение Кеплера оставалось шатким и нестабильным. Как и всех протестантов, его заставили уехать из Граца, после чего он прекратил преподавание и устроился ассистентом к знаменитому (но очень тяжелому в общении) астроному Тихо Браге. Затем он работал главным астрономом при дворе безумного императора Священной Римской империи Рудольфа II – а также был его личным астрологом. После этого наступила черная полоса: жена Кеплера умерла от тифа, дочь – от оспы, сам же ученый после смерти Рудольфа был отлучен от лютеранской церкви за свои воззрения. Вскоре ему пришлось ехать на родину, чтобы защищать свою мать от обвинений в колдовстве (она провела тринадцать месяцев в тюрьме, затем была отпущена на свободу, но прожила по возвращении домой совсем недолго). Несмотря на все это, он продолжал работать. По завещанию Браге ему достался весь архив астронома (но ни одного инструмента из тех, с помощью которых он был собран), и Кеплер решил во что бы то ни стало извлечь из этого максимальную пользу. В любом случае его главный талант состоял не в том, чтобы собирать информацию, а в том, чтобы строить предположения (и проверять их) на основании информации, собранной другими.