Бен Орлин - Время переменных. Математический анализ в безумном мире

Вирджиния Вульф отмечала, что время «заставляет растения и животных расцветать и увядать с потрясающей пунктуальностью». Но «не оказывает такого простого эффекта на сознание человека. Более того, его разум работает с одинаковой странностью, независимо от того, в каком времени находится тело».

Мы охотимся за моментами истории, уродуя время. С помощью песочных часов и размеченных свечей мы поделили день на часы. С помощью маятников и передаточных механизмов разбили часы на минуты (слово «минута» означает «малая» [часть часа]) и после этого – на секунды (более мелкая единица второго порядка, мельчайшая часть минуты). Далее мы разложили время на миллисекунды (половина взмаха крыльев мухи), микросекунды (яркий проблеск стробоскопа) и наносекунды (за каждую из которых свет совершает путешествие на 30 сантиметров), не говоря уж о пико-, фемто-, атто-, зепто- и йоктосекундах. Затем поток названий истощился, предположительно потому, что у доктора Сьюза кончились идеи, но мы продолжаем «мельчить» время. В конце концов вечность распадается на единицы планковского времени, составляющие примерно одну миллиардную триллионной доли йоктосекунды, или количество времени, необходимое для того, чтобы свет прошел 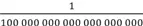пути через протон. Ни один инструмент не может выйти за пределы этой максимальной краткости: физики настаивают, что это наименьшая значимая единица времени, насколько мы можем его понимать (или, как я, не понимать).

Где же, где же ты, мгновение? Где-то за планковским временем? Если мы не можем ни собрать моменты в интервалы, ни разбить интервалы на моменты, так чем же тогда являются эти невидимые, неделимые вещи? Пока я пишу книгу в обычном мире бегущего времени, в каком же искрящемся немире создает свое произведение Хладик?

В XI в. математики впервые нащупали ответ на этот вопрос. В то время как европейские мудрецы рвали на себе волосы, пытаясь рассчитать дату Пасхи, индийские астрономы занимались предсказанием солнечных затмений. Им требовалась ювелирная точность. Астрономы начали членить единицы времени так давно, что прошло почти 1000 лет, прежде чем появились какие-то приборы, которые могли бы их измерить. Одна трути равна менее чем 1/30 000 секунды.

Эти бесконечно малые частицы времени проложили дорогу к понятию, которое называется таткалика-гати – мгновенное движение. Как быстро и в каком направлении движется Луна в данный конкретный момент ?

А что насчет этого момента?

А как сейчас ?

А сейчас ?

В наши дни таткалика-гати известна под более скучным названием – производная.

Возьмем движущийся велосипед. Производная измеряет, как быстро изменяется его положение, то есть скорость велосипеда в отдельно взятый момент. На графике внизу это отражается в кривизне линии. Более крутая кривая указывает на более быстрый велосипед и, таким образом, бо́льшую производную.

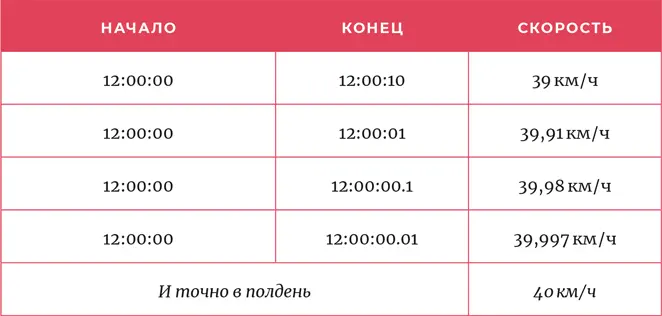
Конечно, в любой отдельно взятый момент велосипед, как и стрела Зенона, неподвижен. Таким образом, мы не можем рассчитать производную в застывшем кадре. Вместо этого мы работаем с помощью сокращения интервала. Во-первых, определим скорость велосипеда в десятисекундный интервал, затем попробуем интервал в одну секунду, затем – 0,1 секунды, 0,01 и 0,001…

Таким хитрым способом мы незаметно подкрадываемся к мгновению, подступаем все ближе, ближе и ближе, пока рисунок не проступает совершенно явственно.

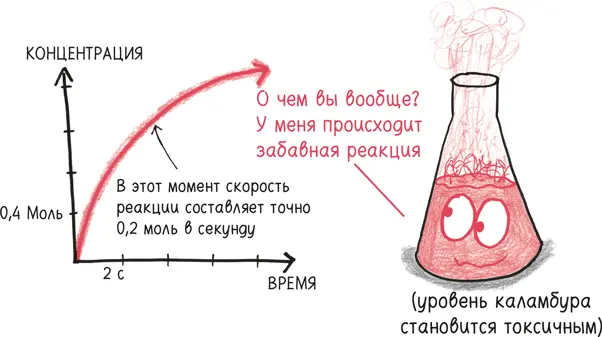
Для другого примера возьмем реакцию синтеза, когда два элемента соединяют свои молекулы, чтобы создать новый химический элемент. Производная измеряет, как быстро растет концентрация вещества, то есть скорость реакции в отдельно взятый момент.

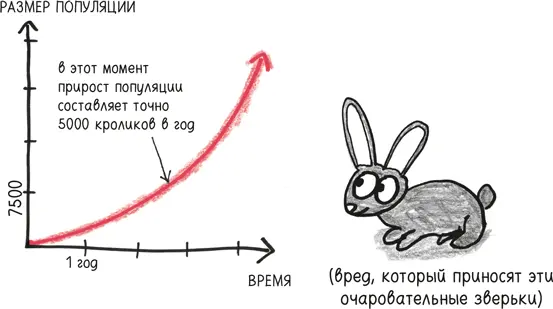
Или представим себе остров, переполненный кроликами. Производная измеряет, насколько быстро меняется размер популяции, то есть скорость ее роста в данный конкретный момент. (Для этого графика мы должны на непродолжительное время принять выдумку о «дробных кроликах», но если ваша вера в невероятное зашла столь далеко, то, я уверен, вы справитесь с любой задачей.)

Этот «хлеб с маслом» всех математиков странным образом похож на поэтическую фантазию. Производная – «мгновенное изменение», она захватывает движение в отдельный момент, как будто ловит молнию в бутылку. Это отрицание Зенона, который сказал, что в отдельно взятое мгновение ничего случиться не может, и оправдание Хладика, который верил, что за один момент может произойти все что угодно.

Теперь, вероятно, вы можете себе представить, как закончилась история Хладика. 12 месяцев он сочинял свою пьесу. «Он трудился не для потомства, – говорит Борхес, – даже не для Бога, чьи литературные вкусы были ему неведомы». Он писал для себя. Он работал, чтобы удовлетворить то, что Томас Вулф считал вечной жаждой художника:

…Навечно закрепить в нерушимых структурах единственный момент человеческого бытия, единственный момент красоты жизни, страсти и неописуемого красноречия, который проходит, загорается и гаснет, всегда просачиваясь сквозь наши пальцы с течением песчинок времени, навсегда ускользающих от нашей отчаянной хватки, ибо река течет и удержать ничего нельзя.

Хладику удалось удержать реку. Не имеет никакого значения, что «Врагов» никто никогда не прочтет или что пули через краткий промежуток времени возобновят свой путь. Важно только то, что он дописал книгу, которая теперь будет существовать всегда, в этот единственный момент, который сам по себе является вечностью.

Исаак Ньютон был любопытным ребенком. Здесь под «любопытным» я подразумеваю «жадным до знаний», а также «очень странным». В одной из историй говорится, что чтение так захватывало юного гения, что его домашняя кошка растолстела, подъедая нетронутые завтраки, обеды и ужины. Или вспомните о том, как он впервые провел исследование по оптике. Встречали ли вы когда-нибудь настолько любопытного ребенка, чтобы он рискнул своим зрением ради проблеска истины? В своем дневнике Ньютон писал: «Я брал шпильку [палочку с тупым концом] и вдавливал ее между глазом и костью, как можно ближе к боковой части глаза. Нажатие… приводило к появлению нескольких светлых, темных и цветных кругов».