Бен Орлин - Время переменных. Математический анализ в безумном мире

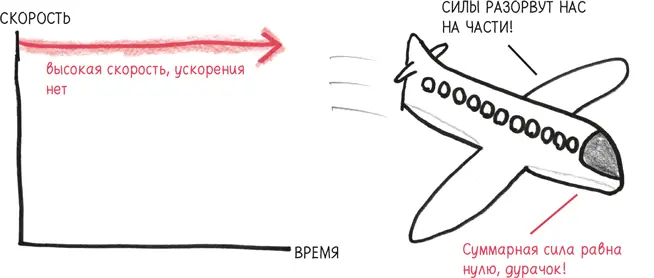
(Как показывают эти примеры, скорость оказывает не очень большое влияние на наши тела. Биомеханическое значение – то, что сдавливает, вызывает тошноту, замешательство и восторг, – имеет ускорение, так как оно представляет собой воздействующую на нас силу.)

«Поэзия начинается с тривиальных метафор, – написал однажды Роберт Фрост, – затем идут недурные метафоры, "изящные" метафоры, пока, наконец, не приходит черед глубоких размышлений». Не уверен, что Фрост нашел бы много поэтического в производных – они являются безнадежно прямыми, говорят только об одной вещи с досадной точностью, – но почва здесь богата метафорами. Если скорость говорит нам об изменении положения, то и ускорение говорит об изменении скорости, и точно так же соответствующая производная указывает на изменения в счастье.

Джеймс – не последний знаток метафор – знал, какой вопрос нужно задать следующим:

– А что насчет третьей производной?

В физике третья производная ( p´ ´´, или « p три штриха») называется рывком. Она определяет изменение в ускорении, которое приводит к изменению силы, воздействующей на тело. Представьте себе мгновение, когда водитель резко нажимает на тормоза автомобиля, или момент отрыва ракеты от пусковой установки, или микросекунду, когда кулак врезается в лицо. Появляется новая сила. Ускорение меняется.

Я никогда не обучал рывку, кроме как в книгах. Три производных – это чертовски много. «Конечно, тот, кто может усвоить вторую или третью флюксию, – писал философ XVIII в. Джордж Беркли, используя термин, который Ньютон применял для производных, – как я думаю, разберется с любой проблемой божественной природы».

– Это довольно сложно понять, – предупредил я Джеймса. – Физическое объяснение достаточно хитрое.

Но в следующие пять минут я пересмотрел взгляды, заполучив в свои сети ярого приверженца математического анализа.

– Не сдавайся! – выкрикнул Джеймс. – Третья производная – это просто: это изменение в изменении изменения моего счастья.

Он говорил все громче, коллеги уже с тревогой оглядывались на нас.

– На самом деле я должен получить все производные! Бесконечный каталог чисел, описывающий, как меняется мое счастье, и как меняется изменение, и как меняется изменение изменения… Тогда мои друзья смогут точно понять, как я себя чувствую, даже без единого слова.

– Это так, – сказал я. – По правде говоря, если они будут точно знать, как изменяется твое счастье в данный конкретный момент – всю бесконечную цепочку производных, – тогда они смогут предсказать твое эмоциональное состояние как угодно далеко в будущем. При наличии достаточного количества производных они смогут рассчитать твое счастье до конца жизни.

– Еще лучше! – Джеймс бешено рассмеялся и захлопал в ладоши. – Мне больше никогда не придется говорить с друзьями!

Я забеспокоился:

– А не окажет ли это само по себе отрицательное воздействие на твой уровень счастья?

Джеймс отмел все возражения:

– Я просто выражу все в производных. Они поймут.

И тут прозвенел звонок. Даже учительский рай приходится иногда покидать, чтобы провести уроки. Отправляясь в класс, я оставил чайную чашку на стойке. Надеюсь, я пробормотал слова благодарности Саре – женщине, которая готовила для нас бутерброды и мыла посуду, – но, зная о своих дурных привычках в то время, могу сказать, что случались дни, когда я забывал это сделать.

Я люблю изобретать математические слова. По крайней мере, мне нравится пытаться это делать. Жестокая правда состоит в том, что канселтарсис (от англ. сancel – отмена) и алгебраж (пламенный гнев из-за того, что пришлось потратить несколько часов на поиск крошечной алгебраической ошибки) так до сих пор и не прижились. Увы, есть и другие вещи, в которых достижения Готфрида Лейбница превышают мои скромные успехи, поскольку именно он ввел в математический лексикон такие слова, как:

● константа (постоянная) – величина, которая не изменяется;

● переменная – величина, которая изменяется;

● функция – правило, устанавливающее соотношение между данными на входе и на выходе;

● производная – одномоментная величина изменений [7] Русский термин «производная» впервые был употреблен В. И. Висковатовым, который таким образом перевел на русский язык французское слово derivee, используемое в учебнике Лагранжа. – Прим. науч. ред. ;

● математический анализ – система исчисления, которую он разработал.

А если еще перечислить символы, которые Лейбниц, хотя и не придумал, но ввел во всеобщий обиход (например, ≅ для конгруэнтности, = для равенства и использование скобок для группировки), то становится ясно, что, делая математическую запись в XXI в., мы идем путем Лейбница, проложенным в XVII в. Но даже если это и так, все вышеперечисленные достижения – всего лишь примечания к его самому значительному вкладу из всех.

Букве d .

Это звучит ужасающе просто. Больше напоминает «Улицу Сезам», чем Гарвард Ярд [8] Гарвард Ярд – старейшая часть кампуса Гарвардского университета. – Прим. пер. . «Все, что Лейбниц сделал, – это поставил d перед х , – шутил легендарный математик сэр Майкл Атья в 2017 г. – Очевидно, таким образом можно стать знаменитым».

Если уж быть справедливым, то любой ощутимый прорыв для удобства обозначений в ретроспективе кажется очевидным. Как часто вы благодарите Роберта Рекорда, изобретателя знака =, позволившего нам опускать бесконечные «равняется»? Цель математических символов – позволить нам перенести мысли на бумагу. Удачно выбранные обозначения ощущаются столь естественными, что вы забываете об искусственности всего процесса. Не стоит заблуждаться: математическая система обозначений – это технологическое достижение, расширение возможностей нашего мозга другими средствами, такое же сверхъестественное и значительное, как роботизированная конечность.

И никто в истории не изобретал символов, обладающих той же наглядной ясностью, как нововведения Готфрида Лейбница. «Подозреваю, что своими успехами в математике, – размышляет специалист в области информационных технологий Стивен Вольфрам, – Лейбниц в значительной степени обязан тому, что вложил немало сил в систему обозначений».

Родившийся в 1646 г., всего через несколько лет после Ньютона, «сооснователя» математического анализа, Лейбниц проявил себя в самых разнообразных областях. Философ, человек, ведущий светский образ жизни, и, как показывают портреты, обладающий головой, на которую возлагались гигантские парики, он мог бы включить «изобретение математического анализа» всего лишь одной строкой в свое резюме. Он был самым известным в Европе специалистом по геологии, Китаю, сложным юридическим вопросам, то есть, если говорить обобщенно, самым известным специалистом в Европе. Один королевский заказчик с тяжелым вздохом называл Лейбница «мой живой словарь». За свою жизнь ученый написал 15 000 писем более чем 1000 корреспондентов.