Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

Алгоритм, прогнозирующий выживание, может на первый взгляд показаться странным выбором проблемы в рамках стандартного цикла PPDAC, поскольку такая ситуация вряд ли возникнет снова, поэтому не представляет никакой ценности для будущего. Но один человек помог мне найти мотивацию. В 1912 году Фрэнсис Сомертон уехал из Илфракомба в Северном Девоне, расположенного недалеко от того места, где я родился и вырос. Отправившись искать счастье в США, он купил билет третьего класса за 8 фунтов и 1 шиллинг на новенький «Титаник», оставив в Европе жену и маленькую дочь. Однако так и не добрался до Нью-Йорка – его надгробие находится на церковном кладбище в Илфракомбе (рис. 6.1). Точный прогнозирующий алгоритм сможет сказать нам: Фрэнсису Сомертону действительно просто не повезло или его шансы на самом деле были невелики.

Рис. 6.1

Надгробие Фрэнсиса Сомертона на кладбище в Илфракомбе. Надпись гласит: «Также Фрэнсис Уильям, сын вышеуказанного, который погиб при катастрофе “Титаника” 14 апреля 1912 года в возрасте 30 лет»

План – собрать имеющиеся данные и попробовать ряд различных методов для создания алгоритмов, предсказывающих тех, кто выжил. Это можно считать скорее проблемой классификации, чем прогнозирования, поскольку все события уже случились. Данные – это открытая информация о 1309 пассажирах «Титаника»: потенциальные предикторные (предсказывающие) переменные включают их полное имя, форму обращения, пол, возраст, класс на судне (первый, второй, третий), сумму, уплаченную за билет, были ли они частью семьи, место посадки на судно (Саутгемптон, Шербур, Куинстаун), а также неполные данные о некоторых номерах кают [125]. Зависимая переменная – это указатель, выжил человек (1) или нет (0).

На этапе анализа важно разделить данные на две части: тренировочный набор, используемый для создания алгоритма, и тестовый набор, который служит только для оценки эффективности – смотреть на тестовый набор до готовности алгоритма было бы серьезным жульничеством. Как и в конкурсе Kaggle, мы возьмем в качестве тренировочного набора случайную выборку из 897 случаев, а оставшиеся 412 человек составят тестовый набор.

Это реальные, а потому довольно загрязненные данные, требующие определенной предварительной обработки. У восемнадцати пассажиров отсутствует информация о плате за поездку, так что будем считать, что они заплатили медианную стоимость для своего класса. Были добавлены некоторые родители, братья и сестры для создания единой переменной, характеризующей размер семьи. Упростились обращения: «мадемуазель» было объединено с «мисс», «мадам» – с «миссис», и целый ряд обращений был закодирован как «редкие формы обращений» [126].

Следует пояснить, что даже для простой подготовки данных к анализу, кроме требуемых навыков кодирования, могут понадобиться серьезные знания и рассуждения – например, об использовании доступной информации о каютах для определения их положения на судне. Несомненно, я мог бы сделать эту работу лучше.

На рис. 6.2 показаны доли выживших для разных категорий из 897 пассажиров, выбранных в качестве тренировочного (обучающего) набора. Все эти признаки сами по себе обладают прогностической способностью: видно, что уровень выживаемости выше среди тех, кто путешествовал более высоким классом; среди женщин и детей; тех, кто больше заплатил за билет; среди имевших небольшую семью и тех, к кому обращались миссис, мисс или мастер [127]. Все это соответствует нашим предположениям.

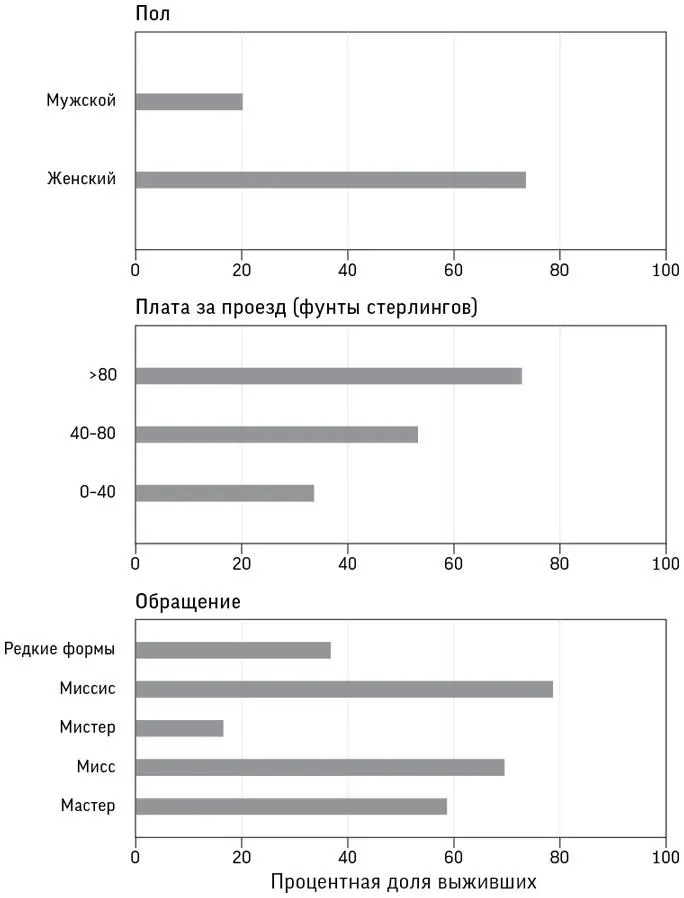
Рис. 6.2

Сводные данные о выживании для тренировочного набора из 897 пассажиров «Титаника», показывающие процентную долю выживших для различных категорий людей

Однако эти параметры нельзя назвать независимыми. Пассажиры более высокого класса предположительно больше заплатили за билеты; можно также ожидать, что у них меньше детей, чем у бедных эмигрантов. Многие мужчины плыли в одиночку. Важным может быть и способ кодирования информации: следует ли рассматривать возраст как качественную переменную с делением на категории (см. рис. 6.2) или как непрерывную переменную? Участники конкурса потратили много времени на подробное рассмотрение таких деталей и кодирование с извлечением максимума информации, но мы перейдем прямо к прогнозированию.

Предположим, мы сделали (заведомо неверный) прогноз: «Никто не выжил». Тогда, учитывая, что зафиксирована смерть 61 % пассажиров, показатель правильности нашего прогноза для тренировочного набора данных составил бы 61 %. Если бы мы строили прогноз на более сложном правиле «Все женщины выживают, а все мужчины погибают», то мы бы верно классифицировали 78 % данных в тренировочном наборе. Эти примитивные правила – хорошие ориентиры, по которым можно измерять все улучшения, обеспечиваемые более изощренными алгоритмами.

Деревья классификации

Дерево классификации – пожалуй, самая простая форма алгоритма, поскольку состоит из серии вопросов типа «да/нет», где ответ на каждый вопрос определяет формулировку следующего вопроса, и так до тех пор, пока не будет получено заключение. На рис. 6.3 показано дерево классификации для данных по «Титанику», в котором в конце каждой ветки указана доля выживших для соответствующей категории. Легко видеть и выбранные факторы, и окончательный вывод. Например, Фрэнсис Сомертон в базе данных отмечен как «мистер», а потому попадает на левую ветвь. Окончание этой ветки включает 58 % данных тренировочного набора, из которых 16 % выжило. Поэтому мы можем оценить на основании ограниченной информации, что шансы на выживание у Сомертона составляли 16 %. Наш простой алгоритм определяет две группы с более чем 50-процентными шансами на выживание. Во-первых, это женщины и дети в первом и втором классе (если у них нет редкой формы обращения), 93 % которых спаслись. Во-вторых, женщины и дети в третьем классе, при условии, что они не из многодетных семей, – из них выжило 60 %.

Рис. 6.3

Дерево классификации для данных по «Титанику», в котором последовательность вопросов приводит пассажиров к концу ветви, где указаны доли выживших для групп из тренировочного набора. Согласно прогнозу, конкретный человек выживет, если в аналогичной группе доля выживших превышает 50 %. Такой прогноз предлагается только для двух категорий пассажиров: женщин и детей из третьего класса из небольших семей, а также всех женщин и детей из первого и второго класса – при условии, что у них нет редких форм обращений

Прежде чем смотреть, как реально конструируется такое дерево, нам нужно решить, какие показатели эффективности следует использовать в нашем конкурсе.