Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

Есть два способа выбраться из этого круга. Первый – сделать какие-то математические предположения о форме исходного распределения в генеральной совокупности, а затем с помощью методов теории вероятностей определить ожидаемый разброс для нашей оценки, а потом и то, чего можно ожидать для разницы между средним в выборке и средним во всей совокупности. Это традиционный способ, который включают в учебники по статистике; мы рассмотрим в главе 9, как он работает.

Но есть и альтернативный подход, основанный на правдоподобном предположении, что вся популяция должна быть примерно схожа с выборкой. Поскольку мы не можем извлечь еще несколько выборок из общей популяции, возьмем несколько раз новые выборки из нашей выборки!

Мы можем проиллюстрировать эту идею на примере нашей предыдущей выборки размером 50, показанной на верхней диаграмме на рис. 7.2; ее среднее значение равно 10,5. Предположим, что мы берем еще 50 точек, каждый раз с возвратом уже взятого наблюдения, и получаем распределение, показанное на второй диаграмме, где среднее значение равно 8,4. Обратите внимание, что это распределение может содержать только те величины, которые есть в исходном распределении, но количество таких наблюдений будет другим, поэтому форма распределения будет слегка отличаться, а вместе с ней будет немного отличаться и среднее. Процесс можно повторять; на рис. 7.2 отображены три повторные выборки, средние значения которых равны 8,4, 9,7 и 9,8.

Рис. 7.2

Исходная выборка из 50 наблюдений и три «бутстрэп-выборки» [154], каждая из которых состоит из 50 наблюдений, извлеченных случайным образом из исходного набора, каждый раз с возвратом. Например, наблюдение в 25 партнеров в первоначальной выборке встречается один раз (справа). В первой и второй бутстрэп-выборках его не оказалось вовсе, а в третьей встретилось дважды

В результате мы получаем представление, как при перевыборках изменяется наша оценка. Процесс известен под названием бутстрэппинг – волшебная идея вытягивания себя за ремешки на обуви сопоставляется со способностью извлекать информацию из самой выборки без предположения о форме распределения всей генеральной совокупности [155].

Если мы повторим эту процедуру, скажем, 1000 раз, то получим 1000 возможных оценок среднего. Они представлены в виде гистограммы на второй панели на рис. 7.3. Остальные гистограммы отражают бутстрэппинг для других выборок на рис. 7.1, при этом каждая гистограмма показывает разброс бутстрэп-оценок вокруг среднего в исходной выборке. Это выборочные распределенияоценок, поскольку они отражают разброс оценок, появляющийся вследствие повторных составлений выборок.

Рис. 7.3

Распределение средних значений для 1000 бутстрэп-выборок, построенных для размеров 10, 50, 200 и 760, отображенных на рис. 7.1. Разброс значений для среднего уменьшается по мере роста размера выборки

Рис. 7.3 отражает некоторые очевидные особенности. Первая и, возможно, самая примечательная – исчезновение практически всех следов асимметрии исходных выборок: распределения для оценок, основанных на данных из повторных выборок, почти симметричны относительно среднего в исходных данных. Это следствие центральной предельной теоремы, которая гласит, что распределение выборочных средних по мере увеличения размера выборки сходится к нормальному распределению – практически вне зависимости от формы исходного распределения данных. Этот важнейший результат мы рассмотрим в главе 9.

Важно отметить, что эти бутстрэп-распределения позволяют количественно выразить нашу неопределенность в оценках, показанных в табл. 7.1. Например, мы можем найти диапазон, который будет содержать 95 % средних в бутстрэп-выборках, и назвать его 95-процентным интервалом неопределенности для исходных характеристик, или погрешностью. Соответствующие интервалы показаны в табл. 7.2 – симметрия бутстрэп-распределений означает, что интервалы неопределенности расположены примерно симметрично вокруг исходной оценки.

Таблица 7.2

Выборочные средние для числа сексуальных партнеров за всю жизнь, указанного мужчинами в возрасте 35–44 лет в исследовании Natsal 3, для вложенных выборок размера 10, 50, 200 и полных данных о 760 мужчинах, с 95-процентными интервалами неопределенности, также называемыми погрешностями

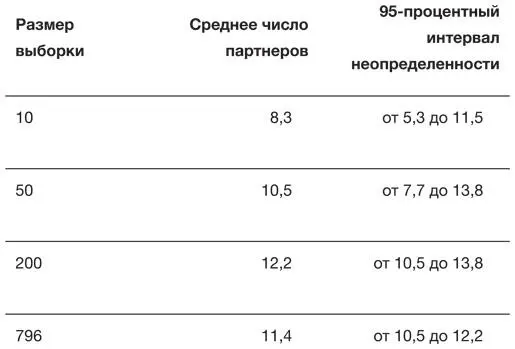
Вторая важная особенность рис. 7.3 – сужение бутстрэп-распределений по мере роста выборки, что отражено в постепенном уменьшении размера 95-процентных интервалов неопределенности.

В этом разделе вы познакомились с некоторыми сложными, но важными идеями:

• разброс в статистиках, основанных на выборках;

• бутстрэппинг данных, когда мы не хотим делать предположения о форме распределения в генеральной совокупности;

• тот факт, что форма распределения статистики не зависит от формы исходного распределения, из которого взяты наблюдения.

Весьма примечательно, что всего это мы достигли без помощи математики, за исключением идеи брать наблюдения случайным образом.

Теперь я покажу, что бутстрэппинг можно применять и в более сложных ситуациях.

В главе 5 мы проводили линии регрессии для данных Гальтона о росте, что позволяло предсказывать, например, рост дочерей на основе роста их матерей с помощью регрессионной прямой с угловым коэффициентом 0,33 (см. табл. 5.2). Но насколько мы можем быть уверены в положении такой прямой? Бутстрэппинг предоставляет интуитивно понятный способ ответить на этот вопрос, не делая никаких предположений о генеральной совокупности, из которой взяты наблюдения.

Составим из 433 пар дочь/мать (рис. 7.4) повторную выборку из 433 элементов (с возвратом) и построим для нее прямую наилучшего соответствия по методу наименьших квадратов. Повторим процедуру столько раз, сколько считаем нужным: рис. 7.4 показывает построенные всего по 20 таким перевыборкам линии наилучшего соответствия, чтобы продемонстрировать их разброс. Поскольку исходный набор данных велик, разброс у этих прямых относительно небольшой – при 1000 бутстрэп-выборках угловой коэффициент с вероятностью 95 % лежит в интервале от 0,22 до 0,44.

Рис. 7.4

Регрессионные прямые для 20 перевыборок из данных Гальтона о росте матерей и дочерей, наложенные на исходные данные. Из-за большого размера выборки угловой коэффициент прямых изменяется относительно слабо

Бутстрэппинг обеспечивает интуитивно понятный, удобный для использования компьютера способ выразить неопределенность в оценках, не делая сильных предположений и не используя теорию вероятностей. Однако этот метод неэффективен, когда нужно найти, например, погрешность в опросе 100 тысяч человек о безработице. Хотя бутстрэппинг – простая, блестящая и крайне эффективная идея, перерабатывать с его помощью такие огромные объемы данных неудобно, особенно при наличии теории, которая может предоставить готовые формулы для величины интервалов неопределенности. Но прежде чем мы ее рассмотрим в главе 9, познакомимся с восхитительной, хотя и непростой теорией вероятностей.