Хорди Деулофеу - Дилемма заключенного и доминантные стратегии. Теория игр

Далее мы изложим эти свойства и покажем их на примере игры в кости. Многие из этих свойств зародились в уже упоминавшейся переписке Паскаля и Ферма, а затем были сформулированы Лапласом в его трудах по теории вероятностей.

Рассмотрим одну из первых задач в теории вероятностей. Роман и Павел играют в азартную игру, выигрывает тот, кто первым наберет 10 очков. В каждом раунде оба имеют равные шансы на победу. Победитель раунда получает 1 очко. После 17-й партии Павел выигрывает со счетом 9:8, после чего игру решено прекратить. Так как никому не удалось набрать 10 очков, игроки решают разделить сделанные ставки. Как справедливо разделить деньги между игроками? «Правильное» решение задачи может зависеть от многих факторов, в том числе не относящихся к математике, поэтому может существовать несколько «допустимых» решений. Однако если мы проанализируем вероятность выигрыша обоих игроков, то сможем справедливо разделить ставки.

До окончания игры нужно сыграть еще максимум две партии. Существует четыре возможных (и равновероятных) результата этих двух партий: (П, П), (П, Р), (Р, П), (Р, Р), где П означает победу Павла, Р — победу Романа. В трех возможных исходах победа останется за Павлом, которому до победы остается всего одно очко, и лишь единственный (последний) исход принесет победу Роману. Поэтому ставки нужно поделить в соотношении 3:1, то есть отдать 3/4 денег Павлу и 1/4 — Роману.

Еще одна задача, о которой идет речь в переписке Паскаля и Ферма, касается азартной игры: нужно решить, как разделить ставки между игроками, если игра прерывается в определенный момент. Эту задачу пытался решить еще Кардано. В его решении разделение ставок зависело от того, сколько очков у каждого игрока, а не от вероятности выигрыша в случае продолжения игры до конца.

Вспомним, что вероятность события рассчитывается по следующему правилу: p( события) = число благоприятных исходов/общее число исходов, то есть нужно определить число наблюдений, при которых наступает нужное событие, и разделить его на общее число наблюдений. Иногда подсчитать это отношение очень просто. Например, какова вероятность, что при броске кубика выпадет четное число очков? Из шести возможных исходов лишь три благоприятных (когда выпадает 2, 4 или 6). Следовательно, p( четное) = 3/6 = 0,5. Так как общее число исходов невелико, подсчет можно произвести простым перечислением всех возможных случаев. В других случаях подобные расчеты могут оказаться намного сложнее, поэтому нужно как следует разобраться в ситуации и иметь соответствующие методы для выполнения расчетов. Так, важная часть анализа сложных азартных игр и случайных событий в целом заключается в правильном перечислении всех возможных исходов.

Далее мы проанализируем несколько ситуаций, чтобы показать различные методы расчетов.

В забеге участвуют 12 бегунов. Сколькими способами можно сформировать тройку призеров?

Первое место может занять любой из 12 участников. Для каждого из этих 12 исходов есть И атлетов, которые могут занять второе место. Для каждой пары первого и второго призеров остаются 10 возможных вариантов третьего места. Следовательно, количество различных троек призеров равно 12 * 11 • 10 = 1320.

Мы определили количество групп из трех бегунов, которых можно выбрать из 12 участников забега, при этом порядок выбора имеет значение. Следовательно, тройки 1, 2, 3 и 2, 3, 1 отличаются: они образованы одними и теми же бегунами, но в первой тройке первым пришел бегун номер 1, вторым — номер 2, третьим — номер 3, а во второй тройке первым пришел бегун номер 2, вторым — номер 3, третьим — номер 1.

На языке математики это называется размещением из 12 элементов по 3 и обозначается V 12,3Как мы уже заметили, оно рассчитывается как 12 • 11 • 10. В общем виде размещение из m элементов по n (очевидно, что n < m) рассчитывается так:

V m,n= m • (m - 1) • (m - 2) • ... • (m - n + 1).

Игрок в бридж при раздаче получает 13 карт. Сколькими способами он может упорядочить карты?

Если у игрока 13 карт, то первую по порядку он может выбрать тринадцатью возможными способами, вторую — двенадцатью, третью — одиннадцатью и так далее до последней карты, которую можно будет выбрать единственным способом (она останется последней неупорядоченной). Следовательно, общее число возможных вариантов упорядочения карт равно:

13 • 12 • 11 • … • 3 • 2 • 1 = 13! = 6 227 020 800.

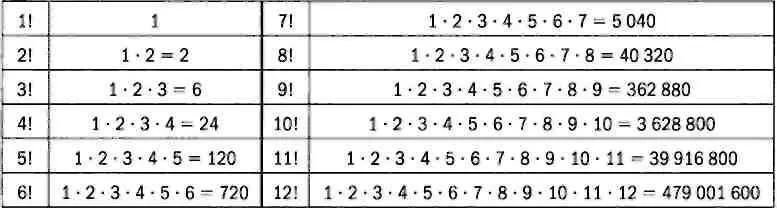
Эта операция называется перестановкой 13 элементов, и результат можно также записать в виде факториала. Факториал обозначается восклицательным знаком после числа. В нашем случае результат равен 13!. По определению n! равен произведению всех натуральных чисел от n до 1. В таблице ниже приведены значения факториала для первых 12 чисел, чтобы дать представление о том, насколько быстро он возрастает.

Подсчет лежит в основе множества карточных игр. Картина Лукаса ван Лейдена «Игроки в карты», 1520 год.

В игре бридж каждому игроку раздается по 13 карт из колоды в 52 карты. Сколькими различными способами можно выдать игроку 13 карт?

В этом случае нужно подсчитать число различных групп по 13 карт, которые можно выбрать из 52 карт, при этом порядок расположения выбранных 13 карт неважен. Если бы порядок карт имел значение, то общее число раздач вычислялось бы так:

52 • 51 • 50 • ... (13 множителей)... * 42 - 41 - 40 = 3,95424 • 10 21.

Но так как порядок карт в раздаче неважен, а каждую группу из 13 карт мы посчитали 13! раз (это число перестановок 13 элементов), число способов раздачи карт в бридже равно

(52 • 51 • ... • 41 • 40)/13! = 52!/(39! • 13!) = 635 013 559 600.

Обратите внимание, что результат выражается огромным числом. В первом случае полученное число имеет 22 цифры в своей записи, во втором (когда порядок неважен) мы получили число из 12 цифр. Это сопоставимо с возрастом Вселенной в 1,5 • 10 10лет или примерно 4,7 • 10 17секунд. Таким образом, первое число (3,9 • 10 21) более чем в 8000 раз превышает число секунд, прошедших с момента Большого взрыва, а второе число (6,3 • 10 11) в 42 раза больше возраста Вселенной в годах.

На языке математики результат этой задачи именуется числом сочетаний из 52 элементов по 13, которое обозначается С 12,13. Как мы уже видели, это сочетание рассчитывается по формуле: 52!/(39! • 13!). Общая формула для вычисления количества сочетаний из m по n (очевидно, что n < m):