Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Возможно, все обстояло именно так, как утверждали Кардано и Феррари. Победа Тартальи над Фиором привлекла внимание Кардано к кубическим уравнениям и дала понять, что решение таких уравнений существует. Затем активные поиски привели его к рукописи дель Ферро, в которой он нашел метод, нужный ему для книги. Вдохновленный открытием, Феррари одолел уравнения четвертой степени. Кардано поместил все это в свою книгу. Феррари, как его ученик, едва ли мог жаловаться на то, что его результаты были туда включены; судя по всему, он даже гордился этим. Из уважения к Тарталье Кардано сослался на него в книге и отдал ему должное за независимое открытие метода и привлечение к нему его, Кардано, внимания.

Книга «Великое искусство» важна еще по одной причине. Кардано применил свои алгебраические методы для нахождения двух чисел, сумма которых равна 10, а произведение 40, и получил ответ: 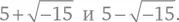Поскольку квадратные корни из отрицательных чисел не извлекаются, он заявил, что этот результат «столь же изящен, сколь бесполезен». Формула для кубических уравнений тоже может давать подобные промежуточные результаты, когда все три решения действительны, и в 1572 г. Рафаэль Бомбелли заметил, что если не обращать внимания на то, что могут означать подобные выражения, и просто просчитать все по формуле, то можно получить верные действительные решения. Со временем это направление мысли привело к созданию системы комплексных чисел, в которой –1 имеет квадратный корень. Без такого расширения системы действительных чисел сегодняшние математика, физика и инженерное дело были бы невозможны.

В 1540-е гг. Кардано вернулся к медицинской практике. Затем (как я уже говорил, его жизнь сплошная мыльная опера и бульварные газеты) разразилась трагедия. Его старший сын Джамбатиста в свое время тайно женился на Брандонии ди Серони – никчемной и бесстыдной, по мнению Кардано-старшего, женщине. Она публично заявляла, что вышла за Джамбатисту только по расчету и что не он отец ее троих детей. Он отравил жену и сразу же сознался в этом. Судья заявил, что единственный способ для Джамбатисты избежать смертной казни – это договориться с семейством ди Серони о материальной компенсации. Кардано-старший попытался это сделать, но запрошенная сумма оказалась настолько огромной, что он не смог заплатить; по приговору суда его сына пытали, затем отрубили ему левую руку и обезглавили.

Кардано – тертый калач, многое повидавший, – вынужден был переехать в другой город; он стал профессором медицины в Болонье. Из-за своего высокомерия Кардано рассорился с коллегами-медиками, и они попытались добиться его удаления из университета. Его младший сын Альдо стал игроком, залез в огромные долги, а затем проник в дом отца и украл у него деньги и драгоценности. Кардано счел себя обязанным сообщить о краже властям, в результате чего Альдо был изгнан из Болоньи. Тем не менее Кардано оставался оптимистом и писал, что, несмотря на эти трагические события, ему «досталось так много милостей, что, выпади они на долю другого человека, тот счел бы себя счастливым». Но у судьбы для Кардано были припасены уже новые катастрофы, и причиной их стали его занятия астрологией. В 1570 г. он составил гороскоп Иисуса Христа. Кроме того, он написал книгу, в которой хвалил Нерона, организовывавшего гонения на первых христиан. Такая комбинация привела к обвинению в ереси, что неудивительно. Кардано был заключен в тюрьму, затем освобожден, но при этом ему было запрещено занимать какой бы то ни было академический пост.

Он отправился в Рим, где, к своему немалому удивлению, встретил теплый прием. Папа Григорий XIII, судя по всему, даровал ему прощение – и пенсию. Кардано был принят в Римскую коллегию врачей и написал – хотя и не опубликовал – автобиографию. В конце концов она была напечатана более чем через 60 лет после его смерти. Согласно легенде, он умер от собственной руки, поскольку предсказал дату своей смерти и профессиональная гордость требовала, чтобы предсказание сбылось.

Мало кому из математиков удается сформулировать задачу, которая несколько столетий остается без решения и при этом оказывается чрезвычайно важной для областей математики, вообще не существовавших на момент ее постановки. Пьер Ферма (частица «де» была добавлена позже, когда он стал правительственным чиновником), возможно, самый известный член этого благородного собрания. Но он, строго говоря, не был математиком: Ферма получил юридическое образование и стал советником парламента в Тулузе. С другой стороны, было бы явной натяжкой назвать его математиком-любителем. Возможно, правильнее всего считать Ферма неоплачиваемым профессионалом, зарабатывавшим на жизнь юридической практикой.

Ферма почти не публиковался, возможно, потому, что нематематические обязанности практически не оставляли ему времени для подробной записи своих открытий. То, что о них известно, мы черпаем в основном из его писем к математикам и философам, таким как Пьер де Каркави, Рене Декарт, Марен Мерсенн и Блез Паскаль. Ферма знал, что такое доказательство; кстати сказать, единственное неверное утверждение в сохранившихся его бумагах (формула, которая, как он считал, всегда выдает простое число) сопровождается замечанием о том, что доказательства у него нет. Из его доказательств почти ничего не сохранилось; самое существенное из дошедшего до нас – доказательство того, что сумма двух квадратов не может быть четвертой степенью, выполненное новаторским методом, который он назвал «методом бесконечного спуска».

Ферма недаром заслужил математическую славу. Он многого добился в геометрии, разработал дифференциальные методы, ставшие предвестниками дифференциального исчисления, работал над теорией вероятностей и математикой в области физики света. Однако главным его достижением стала основополагающая работа по теории чисел. Именно в ней он изложил гипотезу, прославившую его, в том числе и среди обычной публики – отчасти благодаря документальному телефильму и книге-бестселлеру. А именно свою простую, но таинственную Великую или Последнюю (как она известна на Западе) теорему. «Последняя» – не потому, что он прохрипел ее на смертном одре, но потому, что последователи Ферма сумели в течение почти 100 лет после его кончины доказать (или опровергнуть в одном случае) все сформулированные им теоремы за одним-единственным исключением. Эта задачка последней держала оборону, ставя в тупик лучшие умы.