Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков
- Название:Значимые фигуры. Жизнь и открытия великих математиков
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9060-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков краткое содержание
Значимые фигуры. Жизнь и открытия великих математиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
11
В 2009 г. некто Массимо Тарталья ударил статуэткой по лицу премьер-министра Италии Сильвио Берлускони во время его выступления на митинге сторонников. – Прим. ред.
12
Ньютон И. Математические начала натуральной философии. – М.: Наука, 1989.
13
Ньютон И. Математические начала натуральной философии. – М.: Наука, 1989.
14
Ньютон И. Математические начала натуральной философии. – М.: Наука, 1989.
15
Alexandre Koyré. An unpublished letter of Robert Hooke to Isaac Newton, Isis 43 (1952) 312–337.
16
Королевское общество планировало отметить 300-летнюю годовщину рождения Исаака Ньютона в 1942 г., но вмешалась Вторая мировая война, и празднование было отложено до 1946 г. Кейнс подготовил лекцию «Ньютон, человек», но умер незадолго до того, как событие состоялось. За него эту лекцию прочел его брат Джеффри. – Прим. авт.
17
Richard Aldington. Frederick II of Prussia, Letters of Voltaire and Frederick the Great, Letter H7434, 25 January 1778, Brentano’s 1927.
18
«Вот он [ответ]» (лат.). – Прим. ред.
19
Точнее говоря, многочлен должен, помимо всего прочего, быть несократимым – то есть не являться произведением двух многочленов меньшей степени с целыми коэффициентами. Если n – простое число, то x n – 1+ x n – 2+ … + x + 1 несократим всегда. – Прим. авт.
20
Евклид. Начала Евклида. – М., Л.: ГИТТЛ, 1948.
21
Евклид. Начала Евклида. – М., Л.: ГИТТЛ, 1948.
22
Под «солнцами» автор подразумевает звезды с планетными системами. – Прим. ред.
23
Ковалевская С. Воспоминания детства. Нигилистка. – М.: Советская Россия, 1989.
24
Соломон Г. А. Среди красныхъ вождей. Лично пережитое и видѣнное на совѣтской службѣ. – Париж: изд. Мишень, 1930.
25
Пуанкаре А. О науке. М.: Наука, 1990.
26
Пуанкаре А. Указ. соч.
27
В пер. с лат. «с отличием». – Прим. ред.
28
Мастер-формула Рамануджана гласит, что если
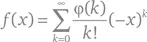
есть комплекснозначная функция, то
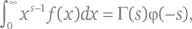
где Г( s ) есть Эйлерова гамма-функция. – Прим. авт.
29
Benoit Mandelbrot. A Maverick’s Apprenticeship, The Wolf Prizes for Physics, Imperial College Press 2002.
30
Benoit Mandelbrot. A Maverick’s Apprenticeship, The Wolf Prizes for Physics, Imperial College Press 2002.
31
В русской традиции этот фрактал получил название «ковер Серпинского». – Прим. пер.
32
Benoit Mandelbrot. A Maverick’s Apprenticeship, The Wolf Prizes for Physics, Imperial College Press 2002.
33
Пусть c = x + iy – комплексное число. Начнем с z 0= 0 и будем считать методом итераций функцию z 2+ c , получая:
z 1= ( z 0 2+ c );
z 2= ( z 1 2+ c );
z 3= ( z 2 2+ c )
и так далее. Тогда c входит во множество Мандельброта в том, и только том случае, если все точки z n лежат в пределах некоторой конечной области комплексной плоскости. То есть множество итераций ограниченно.
34
Сомнительное утверждение. – Прим. ред.
35
https://www.youtube.com/watch?v=zd_HGjH7QZo
36
https://www.youtube.com/watch?v=wO61D9x6lNY
Интервал:
Закладка:










