Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

В том, что так произошло, большая заслуга Пуанкаре, который перешел от резиновых листов к, если так можно выразиться, резиновым пространствам. Метафора листа – двумерная концепция. Если игнорировать все окружающее пространство – как видел его Гаусс, – то для определения точки на листе или, более формально, на поверхности, достаточно двух чисел. Классические топологи, и среди них ученик Гаусса Иоганн Листинг, сумели достаточно подробно разобраться в топологии поверхностей. В частности, они их проклассифицировали, то есть расписали все возможные формы поверхностей, воспользовавшись для этого хитроумным методом конструирования поверхности из плоского многоугольника (и его внутренней части).

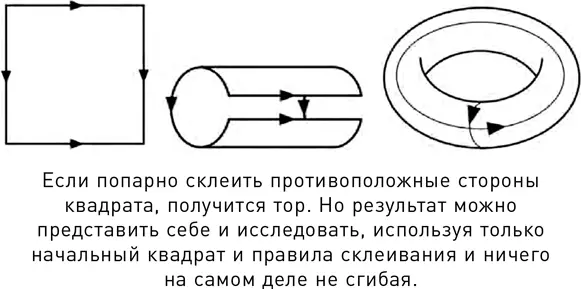
Простой и очень важный пример поверхности – тор. В трехмерном пространстве тор имеет форму бублика с непременным отверстием посередине. Математический тор определяется как поверхность этого бублика – никакого теста внутри, одна только граница с окружающим воздухом. Концептуально эту фигуру можно определить без всякого теста и воздуха. Достаточно взять квадрат и добавить к нему правила, по которым соответствующие точки на противоположных сторонах квадрата тождественны. Если бы вы согнули квадрат и реально склеили противоположные его стороны, вы действительно получили бы поверхность тора. Но можно исследовать все и на плоском квадрате – конечно, если не забывать о правилах. Многие компьютерные игры «загибают» прямоугольный экран, графически используя правила склеивания, так что инопланетные монстры, уходящие за левый край экрана, тут же вновь появляются справа. Никто в здравом уме не будет физически сгибать экран, чтобы получить этот эффект. Этот объект известен в математике под названием, которое явственно отдает оксюмороном, – «плоский тор». Плоский он потому, что его локальная геометрия совпадает с локальной геометрией плоского квадрата. А тор – потому, что его глобальная топология представляет собой топологию… тора.

Иоганн Листинг и другие топологи показали, что любая замкнутая поверхность конечных размеров может быть получена концептуальным склеиванием сторон подходящего многоугольника. Обычно такой многоугольник имеет больше четырех сторон, а правила склеивания могут быть довольно сложными. Исходя из этого, можно доказать, что любая ориентируемая – то есть имеющая две различные стороны, в отличие от знаменитой ленты Мёбиуса, – поверхность представляет собой k -тор, или тор k -го рода. Это поверхность, подобная тору, но с k отверстиями, где k = 0, 1, 2, 3, … Если k = 0, мы получаем сферу, если k = 1, получаем обычный тор, если k ≥ 2, получаем нечто более сложное. Аналогичная классификация существует и для неориентируемых поверхностей, но мы не будем вдаваться в подробности.

Пуанкаре хотел обобщить топологию и распространить ее на пространства размерностей больших, чем два, и очевидным первым шагом в этом направлении был переход к трем измерениям. Здесь принципиальное значение имеет Гауссов объективный взгляд на геометрию; дело в том, что мало смысла в попытках встроить сложное топологическое пространство в обычное трехмерное Евклидово пространство. Это как встраивать тор в плоскость, причем без фокуса с отождествлением сторон. Не получится.

Чтобы понять, что интересные трехмерные топологические пространства – трехмерные многообразия – возможны, мы обобщим прием, которым пользовался еще Листинг. К примеру, чтобы получить плоский трехмерный тор, берут объемный куб (чтобы получить что-то трехмерное, требуется внутренность куба, а не только шесть его квадратных граней) и концептуально склеивают попарно (отождествляют) противоположные грани. Теперь объемный инопланетянин может выйти через одну грань и тут же вновь появиться с противоположной стороны, как если бы эти две грани были двумя сторонами некоего портала в стиле «Звездных врат» и инопланетянин просто проходил бы сквозь этот портал.

В обобщенном смысле мы можем взять многогранник и склеить его грани в соответствии с некоторым набором правил. Этот рецепт позволяет получить множество трехмерных многообразий различных топологий, но таким способом уже невозможно получить их все. (Неочевидно, но это правда.) Мало того, классифицировать топологические типы многообразий с тремя и более измерениями принципиально невозможно; фигур с разной топологией существует слишком много. Но, приложив достаточные усилия, можно выделить кое-какие общие закономерности. В этой связи Пуанкаре принадлежит фундаментальный вопрос, известный как гипотеза Пуанкаре, которую на самом деле, как мы вскоре увидим, лучше было бы назвать ошибкой Пуанкаре, но будем милосердны. В 1904 г. Пуанкаре обнаружил, что некий факт, который он все время неявно полагал очевидным, не был даже верным, и задался вопросом, нельзя ли исправить ситуацию, начав с более сильной гипотезы. Сам он не смог в этом разобраться, лишь заметил, что «этот вопрос увел бы нас слишком далеко в сторону», и оставил головоломку будущим поколениям.

Чтобы понять гипотезу, о которой идет речь, мы для начала рассмотрим аналогичный вопрос в более простом контексте поверхностей: как отличить сферу от всех остальных k -торов? Пуанкаре заметил, что для этого достаточно обратить внимание на одно простое топологическое свойство. Если нарисовать петлю – замкнутую кривую – на сфере, то ее можно непрерывно деформировать, все время оставаясь на сфере, до тех пор, пока она не сожмется в точку. Поскольку в сфере нет отверстий, которые могли бы этому помешать, можно просто сжимать петлю все плотнее и плотнее. Однако на торе k -го рода с одним или несколькими отверстиями (k > 0) петлю, проходящую через отверстие, не удастся сжать в точку. Она в любом случае останется продетой в отверстие.

На языке математики утверждение «любая петля деформируется в точку» обозначается термином «гомотопическая сфера». Мы только что набросали кратко доказательство того, что, если речь идет о поверхностях, любая гомотопическая сфера топологически эквивалентна настоящей сфере. Это позволяет характеризовать сферу при помощи простого топологического свойства. Гипотетический муравей, живущий на поверхности, мог бы, в принципе, разобраться, является ли эта поверхность сферой; для этого ему надо было бы раскладывать всюду веревочные петли и стягивать их в точку. Пуанкаре предположил, что нечто подобное характеризует и трехмерную сферу, или 3-сферу, которая представляет собой трехмерное многообразие, аналогичное сферической поверхности. Это не просто заполненный шар. У шара есть граница, у 3-сферы ее нет. Можно представить себе 3-сферу как шар, поверхность которого стянута в одну точку, – в точности так же, как тонкий диск топологически превращается в сферу, если стянуть все граничные точки в одну. Представьте себе мешок со шнурком вокруг горловины. Когда вы затягиваете шнурок, граница стягивается в точку и мешок приобретает топологию сферы.