Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Все изменилось – вся теория инвариантов буквально встала с ног на голову – в 1888 г., когда Гильберт опубликовал короткую статью, в которой доказывал, что конечный базис всегда существует, вообще не вычисляя никаких инвариантов . Фактически он доказал, что любой подходящий набор алгебраических выражений всегда имеет конечный базис – и неважно, состоит он из инвариантов или нет. Гордан, надо сказать, не ожидал подобного ответа, и, когда Гильберт представил свою работу в Mathematische Annalen , Гордан ее отверг. «Это не математика, – сказал он. – Это теология». Гильберт пожаловался на отказ редактору Клейну и не захотел что-либо менять в статье – разве что возникнут какие-то «конкретные и неоспоримые возражения против моих рассуждений». Клейн согласился опубликовать статью в первоначальном виде. Подозреваю, что он понял доказательство лучше, чем Гордан, который оказался не в своей тарелке, когда способность к вычислениям вдруг сменилась понятийным мышлением.

Несколькими годами позже Гильберт расширил свои результаты и представил в журнал новую статью. Клейн принял ее, охарактеризовав как «важнейшую работу по общей алгебре, которую Annalen когда-либо публиковали». Что же касается Гильберта, то он теперь сделал все, что намеревался сделать в этой области. «Я определенно оставлю область инвариантов», – написал он Минковскому. И оставил.

Доведя до совершенства теорию инвариантов – эта область исследований, по существу, заглохла после того, как с ней поработал Гильберт, и оживилась лишь много лет спустя в еще более общем контексте, причем тогда возродился интерес одновременно и к вычислениям, и к понятиям, – Гильберт нашел для себя новую область приложения сил. В 1893 г. он начал новый проект – «Отчет о числах» ( Zahlbericht ). Дело в том, что Немецкое математическое общество предложило ему исследовать крупную область теории чисел – ту область, где рассматриваются алгебраические числа, то есть комплексные числа, удовлетворяющие полиномиальному уравнению с рациональными (или, что эквивалентно, целыми) коэффициентами. Примером алгебраического числа может служить 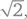удовлетворяющий уравнению x 2–2 = 0; еще один пример – мнимое число i, удовлетворяющее уравнению x 2+ 1 = 0. Как отмечено в главе 16, комплексные числа, которые не являются алгебраическими, называют трансцендентными; примеры таких чисел включают числа π и e, хотя это свойство трудно доказать, и долгое время вопрос оставался открытым. Трансцендентность e доказал Шарль Эрмит в 1873 г., а с трансцендентностью π разобрался Линдеман в 1882 г.

Основную роль алгебраические числа играют в теории чисел. Эйлер неявно использовал некоторые их свойства, к примеру при доказательстве Великой теоремы Ферма для кубов, но систематическое их изучение начал Гаусс. Пытаясь обобщить свой закон квадратичной взаимности на степени выше двойки, он открыл красивое расширение его на четвертые степени, основанное на алгебраических числах вида a + i b , где a и b – целые. Эта система «Гауссовых целых чисел» обладает многими особыми свойствами, в частности, имеет собственный аналог простых чисел и к нему собственную теорему о единственности разложения. Кроме того, Гаусс использовал алгебраические числа, имеющие отношение к корням единицы, при построении правильного семнадцатиугольника.

В главе 6, в связи с Великой теоремой Ферма, мы говорили о том, как использовал алгебраические числа Куммер и какое он предложил понятие идеальных чисел. Дедекинд упростил эту идею, переформулировав ее в терминах особых множеств алгебраических чисел, которые он назвал идеалами. После Куммера теория алгебраических чисел рванула вперед с помощью и при содействии теории уравнений Галуа и так же активно развивающейся абстрактной алгебры (глава 20). Фразу «алгебраическая теория чисел» можно интерпретировать двояко: это может быть и алгебраический подход к теории чисел, и теория алгебраических чисел. Теперь же оба значения сходились к одному и тому же, и именно в этом Немецкое математическое общество просило Гильберта разобраться. Он, что характерно, пошел намного дальше. Он задался вопросом, которым испокон веков задаются математики, столкнувшиеся с большим массивом интересных, но неорганизованных результатов: «Да, конечно, но о чем это на самом деле ?» Поиск ответов на этот вопрос позволил ему сформулировать и доказать множество новых теорем.

Все время работы над «Отчетом о числах» Гильберт вел обширную переписку на эту тему с Минковским – иногда даже слишком обширную, так что временами Гильберт чувствовал настоящее отчаяние; ему начинало казаться, что работа никогда не будет закончена в виде, который удовлетворил бы его взыскательного друга. Однако в конечном итоге отчет был опубликован. В нем были сформулированы и доказаны общие аналоги квадратичной взаимности, образовавшие основу того, что мы сегодня называем теорией полей классов – это до сих пор активно развивающаяся, хотя и весьма сложная технически понятийная основа для теории алгебраических чисел. В предисловии к «Отчетам» говорится:

Таким образом, мы видим, как далеко арифметика – королева математики – зашла в захвате обширных областей алгебры и теории функций, чтобы стать их лидером… Следует заключить, если я не ошибаюсь, что прежде всего современное развитие теоретической математики происходит под знаменем числа.

Возможно, сегодня мы не станем заходить так далеко, но в то время такое заявление было вполне оправданным.

Гильберт, как правило, работал 5–10 лет в одной области, решал в ней крупные задачи, доводил все до совершенства, а затем уходил на новые «угодья», иногда совершенно забывая, что когда-то изучал эту тему. Однажды он заметил, что занимается математикой потому, что в ней, если что-то забудешь, всегда можно вывести это заново. Математик до мозга костей, теперь он «покончил» с алгебраической теорией чисел. И двинулся дальше. Его студенты, которых он из года в год бомбардировал лекциями об алгебраических числах, были поражены, когда выяснилось, что в следующем году темой лекций Гильберта будут начала геометрии. Гильберт возвращался к Евклиду.

Как всегда, у Гильберта были на то свои резоны, и опять же ключевой вопрос можно было сформулировать так: «Да, конечно, но о чем это на самом деле ?» На этот вопрос Евклид дал бы ответ «о пространстве»; именно поэтому он все свои теоремы иллюстрировал геометрическими чертежами. Гильберта, однако, гораздо больше интересовала логическая структура аксиом геометрии и как из них проистекают теоремы, часто далеко не очевидные. Его также не устраивал у Евклида список аксиом, поскольку использование чертежей привело Евклида к некоторым допущениям, которые он не сформулировал явно.