Альфред Реньи - Диалоги о математике

Гиерон . Даже если математическая модель приводит к результатам, отличным от действительности, она может быть полезна, так как недостатки одной модели могут быть учтены при создании другой, лучшей модели. Мне кажется, прикладная математика похожа на войну; иногда поражение ценнее победы, так как помогает найти недостатки нашего оружия или стратегии.

Архимед . Теперь ты действительно постиг существо проблемы.

Гиерон . Расскажи мне что-нибудь еще о своих зеркалах.

Архимед . Я уже изложил тебе основную идею. После того как я пришел к мысли использовать упомянутые свойства параболы, нужно было разрешить проблемы обработки и полировки металлического зеркала в форме вогнутого параболоида вращения, однако я предпочел бы не говорить об этом. Конечно, я также должен был выбрать подходящий сплав.

Гиерон . Даже не вникая в твои секреты, я понял, что, кроме свойств параболы, ты должен многое знать о металлах и об искусстве их обработки. Выходит, что знаний математики недостаточно, если кто-то хочет применять их на деле. Не похож ли человек, желающий применять математику, на человека, пытающегося ехать верхом на двух лошадях одновременно?

Архимед . Я немного тебя поправлю: тот, кто намерен применять математику, похож на человека, который хочет запрячь двух лошадей в одну повозку: И это не так уж трудно сделать. Конечно, при этом необходимы некоторые познания как о лошадях, так и о колесницах, но каждый из твоих возничих обладает подобными знаниями.

Гиерон . Теперь я совершенно запутался: я все время считал, что прикладная математика — это какое-то таинство, а ты показал, что в действительности все очень просто. Но когда я убедился, что это на самом деле просто, ты показал мне, что все гораздо сложнее, чем я себе представлял.

Архимед . Принципы очевидны, но детали иногда бывают очень запутаны.

Гиерон . Я все еще не понимаю, что ты подразумеваешь под математической моделью. Расскажи мне об этом подробнее.

Архимед . Помнишь ли ты сферу, которую я построил несколько лет назад для демонстрации движения Солнца, Луны и пяти планет, с помошыо которой можно показать, как происходят затмения Солнца и Луны?

Гиерон . Конечно, ведь это одна из диковин в моем дворце, которую я показываю всем гостям; каждый думает, что это нечто удивительное. Может быть, это математическая модель Вселенной?

Архимед . Нет. Я назвал бы ее физической моделью. Математические модели невидимы. Они существуют только в нашем сознании и могут быть выражены в формулах. Математическая модель Вселенной — нечто общее между действительным миром и моей физической моделью. В физической модели, например, каждая планета — крошечный шар размером с апельсин. В математической модели Вселенной планеты изображаются просто точками.

Гиерон . Мне кажется, я начинаю понимать, что именно ты имеешь в виду под математической моделью. Вернемся к примеру с лошадьми. Искусство запрягать лошадей и править ими — это совершенно не то, что разводить лошадей. Не является ли искусство прикладной математики чем-то совершенно отличным от открытия и доказательства теорем?

Архимед . Ты, конечно, прав, хотя человек, который выращивает лошадей, обычно знает о них все и может управлять ими лучше, чем кто-либо другой. Что касается математики, то я подчеркнул раньше: для успешного применения нужно глубокое понимание ее, и если кто-то хочет применить математику к новым объектам, он должен быть творческим математиком. И наоборот, интерес к применениям может помочь в чисто математических исследованиях.

Гиерон . Как это возможно? Не приведешь ли ты какой-нибудь пример?

Архимед . Вероятно, ты помнишь, что одно время я очень интересовался механикой, а более точно — нахождением центров тяжести тел. Результаты, которые я получил, помогли мне не только построить механизмы, но и доказать новые геометрические теоремы. Я разработал специальный метод исследования геометрических задач с помощью механики и использования центров тяжести фигур. Метод эвристический — не дающий точного доказательства, но благодаря ему многие теоремы становились мне ясны. Конечно, позднее теоремы, открытые посредством моего механического метода, я строго доказывал традиционными методами геометрии. Найти доказательство значительно легче, если предварительно уже получены некоторые сведения из механических аналогий и, таким образом, известно, что должно быть доказано.

Гиерон . Укажи мне какую-нибудь теорему, которую ты нашел таким странным путем.

Архимед. Площадь любого сегмента параболы равна четырем третям площади треугольника, который имеет то же основание и ту же высоту. После обнаружения результата я доказал его с помощью традиционных методов.

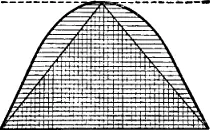
Гиерон . Если ты установил эти теоремы с помощью механики, зачем тебе нужно еще геометрическое доказательство?

Архимед . Когда я открыл мой метод, результаты, полученные с его помощью, были не совсем точны; позднее, анализируя случаи, когда этот метод вводил меня в заблуждение, я настолько развил его, что теперь он никогда не подводит меня. Но я еще не уверен до конца, что результаты, полученные таким путем, действительно верны. Может быть, однажды кто-нибудь докажет это. Но до сих пор я не имею полной уверенности в методе.

Гиерон . Но разве в прикладной математике так уж необходимы строгие доказательства? Ты сказал, что математическая модель — это только приближение к действительности. Если ты используешь приблизительно точную формулу, твои результаты будут все так же приблизительны, и, во всяком случае, они никогда не могут быть абсолютно точными.

Архимед . Ты ошибаешься, мой государь. Именно потому, что математическая модель — это только приближение к действительности и всегда имеется некоторое отличие от нее, нужно остерегаться и не увеличивать это различие еще больше небрежным использованием математики. Надо быть как можно более точным. Кстати, относительно приближений существует общее заблуждение, что использование их означает отклонение от математической точности. Приближения имеют точную теорию, и результаты о приближениях, например неравенства, должны доказываться так же строго, как и тождества. Возможно, ты помнишь приближения для площади круга с заданным диаметром. Я доказал их со строгостью, обычной в геометрии.