Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Тригонометрия основана на ряде особых функций, из которых основными считаются синус, косинус и тангенс. Они применимы к углу, традиционно представленному греческой буквой θ (тета), и могут быть определены в терминах прямоугольного треугольника, чьи три стороны a, b и c соответственно называются прилежащим и противолежащим катетами и гипотенузой.

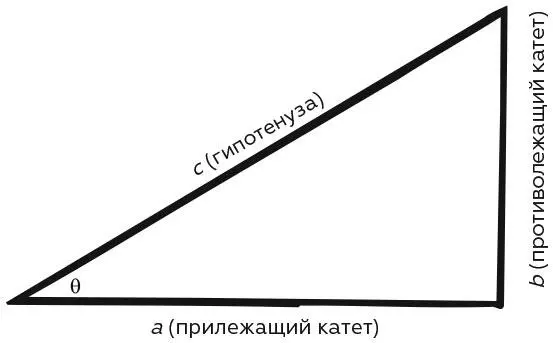
Тогда:

синус тета равен sin θ = b/c ,

косинус тета равен cos θ = a/c ,

тангенс тета равен tan θ = b/a .

Получается, что значения этих трех функций для заданного угла θ определяет геометрия треугольника (одинаковый угол может быть у треугольников разных размеров). Но геометрия подобных треугольников подразумевает, что коэффициент подобия между ними не зависит от их размера. Однако когда эти функции были вычислены и занесены в таблицы, с их помощью стало легко «решать» треугольник (вычислять все его стороны и углы) по величине θ. Взаимоотношения между тремя функциями были описаны множеством красивых формул. В частности, теорема Пифагора заключает в себе следующее:

sin 2θ + cos 2θ = 1.

Судя по всему, тригонометрия ведет происхождение от астрономии, где относительно просто измерить углы, но очень трудно – невообразимые расстояния. Греческий астроном Аристарх в своем труде, датируемом примерно 260 г. до н. э., «О величинах и расстояниях Солнца и Луны», определил, что Солнце удалено от Земли на расстояние, от 18 до 20 раз большее, чем расстояние от Земли до Луны. (Точная цифра ближе к 400, но Евдокс Книдский и Фидий доказывали, что верное число – 10.) Его объяснение было таково: когда Луна достигает половины полного размера, угол между направлениями от наблюдателя к Солнцу и Луне равен примерно 87° (в современных единицах). Используя свойства треугольников, что равнозначно тригонометрической оценке, он определил (в современных единицах), что величина sin 3° лежит между 1/ 18и 1/ 20, что приводит к оценке соотношения расстояний до Солнца и до Луны. Сам метод был верен, не хватало точности наблюдений: точный угол равен 89,8°.

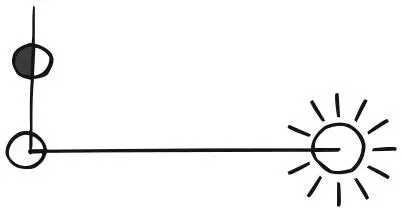
Положение Солнца, Луны и Земли, когда освещена половина Луны

Первые тригонометрические таблицы составил Гиппарх примерно в 150 г. до н. э. Вместо современной функции синуса он использовал очень близкое понятие, что с геометрической точки зрения было совершенно естественным. Представьте себе круг с двумя радиусами, которые образуют угол θ. Конечные точки радиусов на окружности можно соединить прямой, называемой хорда . Также их можно принять как конечные точки дуги окружности.

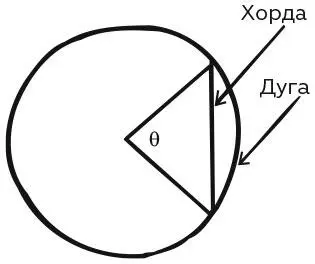
Дуга и хорда, соответствующие углу θ

Гиппарх составил таблицу соответствующих длин дуг и хорд для углов разной величины. Если радиус круга равен 1, то длина дуги равна θ в радианах . Простые геометрические построения демонстрируют, что длина хорды в современной нотации равна 2sin θ/ 2. Итак, мы видим, что вычисления Гиппарха очень близко подводят нас к таблице синусов, хотя они и не были представлены именно в таком виде.

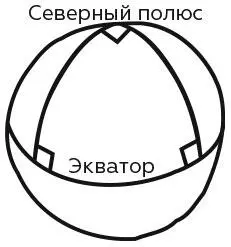
Любопытно, что первые труды по тригонометрии были гораздо сложнее, чем б о льшая часть материала, преподаваемого сегодня в школе, и снова благодаря астрономии (и позже навигации). Здесь мы имеем дело с естественным пространством, которое представляет собой не плоскость, а сферу. Небесные тела можно представить расположенными на воображаемой гигантской сфере. И самым точным представлением о небе будет его внутренняя поверхность, окружающая наблюдателя: на таком расстоянии действительно может показаться, что они лежат на этой сфере.

Как следствие, астрономические вычисления связаны с геометрией сферы, а не плоскости. Соответственно, и требования к ним определяются не плоскостной геометрией и тригонометрией, а геометрией и тригонометрией сферы. Одной из самых ранних работ на эту тему считают сочинение Менелая «Сферика» примерно 100 г. н. э. Пример одной из его теорем, не имеющей аналогов в геометрии Евклида, таков: если два треугольника имеют одинаковые углы, то они конгруэнтны – т. е. совпадают как по размеру, так и по форме (по Евклиду они подобны: имеют одну форму, но, возможно, разные размеры). В сферической геометрии сумма углов треугольника превышает 180°. Например, треугольник, чьи вершины лежат на Северном полюсе и двух точках экватора, разнесенных на 90°, явно имеет три прямых угла, т. е. их сумма равна 270°. И чем больше размеры треугольника, тем больше сумма его углов. Фактически эта сумма минус 180° пропорциональна общей площади треугольника.

Эти примеры показывают, что геометрия сферы имеет свои характеристики и необычные черты. То же относится и к сферической тригонометрии, хотя и здесь основными остаются стандартные тригонометрические функции. Меняются только формулы.

Безусловно, вершиной тригонометрической мысли античности является текст Птолемея Александрийского Megale syntaxis («Великое построение»), датируемый примерно 150 г. н. э. Он больше известен как «Альмагест», что по-арабски означает «величайший», и включает тригонометрические таблицы, снова изложенные в понятиях хорд, вместе с методами вычисления их размеров, а также описание положений светил на небесной сфере. Превосходным примером сложнейшего хода мысли Птолемея служит его теорема, согласно которой если четырехугольник ABCD вписан в окружность (его вершины лежат на этой окружности), то

AB × CD + BC × DA = AC × BD

(произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон).

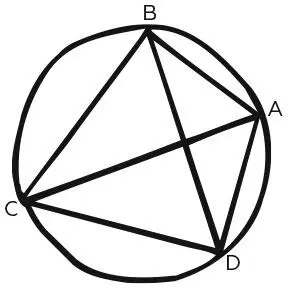
Четырехугольник, вписанный в окружность, и его диагонали

Современная интерпретация этого факта – знаменитая пара формул:

sin (θ + φ) = sin θ cos φ + cos θ sin φ,

cos (θ + φ) = cos θ cos φ – sin θ sin φ.

Главное следствие из этой формулы – возможность легко вычислить синус и косинус суммы двух углов, если вам известны синус и косинус каждого из них. Итак, начиная (например) с sin 1° и cos 1°, вы можете вычислить sin 2° и cos 2°, взяв θ = φ = 1°. Затем вы можете получить sin 3° и cos 3°, взяв θ = 1°, φ = 2°, и т. д. Вам только необходимо знать, как начать, но всё, что вам позже потребуется, не выходит за рамки арифметики. Вычислений будет довольно много, зато они несложные.