Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Джероламо Кардано был незаконным сыном миланского стряпчего Фацио Кардано и молодой вдовы Клары Мичери, вынужденной одной растить троих детей. Дети умерли от чумы в Милане, пока Клара рожала Джероламо в Павии. Фацио был способным математиком и передал Джероламо увлечение этим предметом. Джероламо против воли отца пошел изучать медицину в университете Павии: Фацио хотел, чтобы он тоже стал юристом.

Еще студентомКардано был выбран ректором университета (по местной традиции ректор избирался из студенческой среды) в Падуе, куда он переехал, с перевесом в один голос. Едва успев получить наследство после смерти отца, Кардано промотал все деньги в азартные игры [2] Сомнительно. Отец оставил Кардано небольшое имущество, но право на наследство оспаривалось многими людьми. Кардано выиграл суды, но через 23 года. Кроме того, в силу преимуществ из знания теории вероятностей он обыгрывал людей в азартные игры, причем прилично. Источник: Гутер Р., Полунов Ю. Джероламо Кардано. М., 2010. Прим. науч. ред. : карты, кости и даже шахматы. Он не расставался с кинжалом и однажды ударил им в лицо противника, которого заподозрил в мошенничестве.

В 1525 г. Кардано получает диплом медика, однако ему пришлось покинуть пост в Миланской коллегии врачей – возможно, из-за скандальной репутации. Он практиковал медицину в деревне Сакка и женился на Лючии Бандарини, дочери капитана местного ополчения. Практика не приносила дохода, и в 1533 г. Кардано снова увлекся азартными играми, и на этот раз проигрыш оказался серьезнее: пришлось заложить драгоценности жены и кое-что из фамильной мебели.

Кардано снова повезло: к нему перешло место отца, преподавателя математики в школе Пиатти. По совместительству он продолжал практиковать медицину, и несколько чудесных выздоровлений заметно укрепили его репутацию врача. В 1539 г., после нескольких неудачных попыток, его снова приняли в коллегию врачей. Он начал публиковать учебные тексты по разным темам, в том числе по математике. Кардано написал замечательную автобиографию «О моей жизни» – альманах, составленный из глав на разные темы. Будучи на вершине славы, он получил вызов в Эдинбург, к одру архиепископа Сент-Эндрюса Джона Гамильтона. Гамильтон страдал от жестокой астмы. Но его состояние резко улучшилось после вмешательства Кардано, и медик покинул Шотландию, став богаче на 2000 золотых крон.

Он стал профессором в университете в Падуе, и всё шло прекрасно, пока его старший сын, Джамбаттиста, не женился тайком на Брандонии Серони, «никчемной, бесстыжей женщине», по оценке самого Кардано. Вместе со своей родней она публично унижала и издевалась над Джамбаттистой, и он отравил ее. Несмотря на все старания Кардано, его сына казнили. В 1570 г. Кардано был обвинен в ереси за то, что посмел составить гороскоп Иисуса Христа. Его посадили в тюрьму, затем отпустили, но лишили права преподавать в университете. Он переехал в Рим, где неожиданно получил отпущение грехов у папы и снова был принят в коллегию врачей.

Он предсказал день своей смерти и постарался доказать свою правоту, совершив самоубийство [3] По легенде, Кардано предсказал день своей смерти (лет за сорок до нее) и, чтобы оправдать это и авторитет знаменитого астролога, покончил с собой (по одной версии – уморил себя голодом, по другой – принял яд). На самом деле он умер позже, ошибившись на три года и назначив день своей кончины на декабрь 1573 г. Прим. науч. ред. . Несмотря на всё пережитое, он до самого конца оставался оптимистом.

В XV в. появились первые примитивные символы, прежде всего буквы p и m для сложения и вычитания: plus и minus . Это скорее были сокращения, чем символы. Но и символы + и – появились примерно в то же время. Они пришли из области коммерции, точнее, от немецких купцов, обозначавших перевес или недовес. Математики быстро тоже стали ими пользоваться: первые письменные свидетельства относятся к 1481 г. Уильям Отред ввел символ × для умножения и был безжалостно (и справедливо) раскритикован Лейбницем за то, что его очень легко спутать с буквой x.

В 1557 г. английский математик Роберт Рекорд в своей книге «Точильный камень остроумия» ввел символ = для равенства, используемый по сей день. Он писал, что ему в голову не приходило ничего лучше, чем две параллельные линии равной длины. Правда, у него они были намного длиннее, чем те, которые ставим мы, что-то вроде: . Виет сперва писал вместо равенства слово «aequalis», но позже заменил его символом ~. Рене Декарт использовал другой символ – ∞.

Современные символы > и < для «больше» и «меньше» пришли к нам благодаря Томасу Хэрриоту. Круглые скобки () появились в 1544 г., а квадратные [] и фигурные { } изобрел Виет примерно в 1593 г. Декарт использовал символ квадратного корня √, представляющего стилизованную букву r для обозначения корня; для кубического корня он использовал символ √с.

Чтобы наглядно показать разницу между символами нашего времени и периода Возрождения, приведу цитату из «Великого искусства» Кардано:

5p: R m:15

5m: R m:15

25m: m:15 qd. est 40.

В современных символах получится:

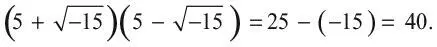
Итак, здесь мы видим p: и m: для плюса и минуса, R для квадратного корня и qd. est для латинского выражения «что есть». Кардано писал

qdratu aeqtur 4 rebus p : 32

там, где мы бы написали

x 2= 4 x + 32.

Он использовал разные сокращения, rebus и aeqtur , для неизвестного (предмета) и его квадрата. В остальных местах он использует R как неизвестное, Z для его квадрата и C для куба.

Влиятельной, хотя и малоизвестной фигурой был в свое время француз Никола Шюке, чья книга «Наука о числах в трех частях» («Le triparty еn la science des nombres»), вышедшая в 1484 г., описывала три главные математические темы: арифметику, корни и неизвестные. Его обозначение для корней очень похоже на символ Кардано, но он первым ввел надстрочное написание степени неизвестного. Он называл первые четыре степени неизвестного premier, champs, cubiez и champs de champs [4] В переводе с французского – «первый», «поверхность», «кубический» и «поверхность на поверхность». Прим. науч. ред. . Для того, что мы бы сейчас написали как 6 x , 4 x 2, 5 x 3, он использовал комбинации.6.1, 4.2 и.5.3. Он также применял ноль и отрицательные степени и писал.2.0 и.3. 1.m., где мы бы написали 2 и 3 x –1. Он использовал экспоненциальную запись (надстрочные символы) для степеней неизвестного, но не символы для самого неизвестного.