Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

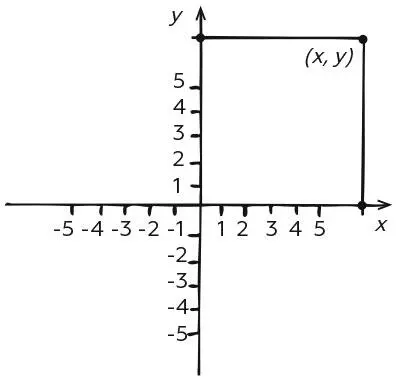
Вдоль каждой оси наносятся целые числа: положительные в одном направлении и отрицательные в другом. Соответственно, горизонтальная ось называется x , а вертикальная y . Символы x и y используются для представления точек с помощью соответствующих осей – это расстояния от начальной точки. Обычная точка на плоскости, на расстоянии x по горизонтальной оси и y по вертикальной, обозначается парой чисел ( x, y ). Эти числа и есть координаты точки.

Любое уравнение, содержащее x и y , накладывает ограничения на возможные точки. Например, если оно выглядит как x 2+ y 2= 1, точка ( x, y ) должна находиться на расстоянии 1 от начальной, согласно теореме Пифагора. Такие точки образуют окружность. Мы скажем, что x 2+ y 2= 1 – уравнение для этой окружности. Любое уравнение соответствует какой-то кривой на плоскости, а любая кривая соответствует уравнению.

Декартовы координаты алгебраически тесно связаны с коническими сечениями – кривыми в геометрии, которые древние греки строили как сечения двойного конуса. Алгебраически получается, что конические сечения являются следующим видом простейших кривых линий после прямых. Прямая линия описывается уравнением

ax + by + c = 0

с константами a, b и c . Коническое сечение описывается квадратным уравнением

ax 2+ bxy + cy 2+ dx + ey + f = 0

с константами a, b, c, d, e, f . Декарт отмечал этот факт, но не смог его доказать. Но он разобрал случай, основанный на теореме, которая приписывалась Паппу и давала характеристики коническим сечениям. Он сумел доказать, что там результат описывается квадратным уравнением.

Он пошел дальше и обратился к уравнениям более высокого порядка, описывая более сложные кривые, чем те, с которыми имела дело классическая греческая геометрия. Типичным примером можно считать декартов лист, задаваемый уравнением:

x 3+ y 3 – 3 axy = 0,

которое описывает петлю с двумя концами, уходящими в бесконечность.

Пожалуй, главный вклад концепции координат проявляется именно в этом: Декарт смог уйти от греческого взгляда на кривые как на объекты, построенные с помощью особых геометрических приспособлений, и увидел в них визуальное представление любой алгебраической формулы. Как заметил в 1707 г. Исаак Ньютон, «современный подход, но намного более глубокий [чем у греков], позволяет любую линию в геометрии выразить в виде уравнения».

Более поздние ученые изобрели множество вариантов декартовой системы координат. В письме от 1643 г. Ферма рассматривает идеи Декарта и развивает их для трехмерного пространства. Он упоминает такие поверхности, как эллипсоид и параболоид, описываемые квадратными уравнениями с тремя переменными x, y, z . Важным вкладом было введение Якобом Бернулли полярных координат в 1691 г. Чтобы определять точки на плоскости, он использовал угол θ и расстояние r вместо пары осей. Теперь эти координаты стали обозначать как ( r , θ).

Декартов лист

И снова уравнения соответствуют определенным кривым. Но теперь простые уравнения могут описать кривые, которые были чрезвычайно сложными в декартовых координатах. Например, r = θ описывает спираль, ту самую, что уже известна нам как архимедова .

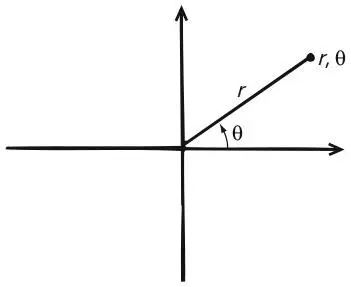
Полярные координаты

Важнейшее применение координат в математике – метод графического представления функций.

Функция – не число, но отношение между элементами, когда изменение в одном влечет перемены в другом. Оно часто выражается в формуле, которая приписывает каждому числу, x (возможно, с предварительными ограничениями), другое число, f(x ).

Например, функция квадратного корня определяется правилом f ( x ) = √ х , т. е. извлечением квадратного корня из данного числа. Это отношение требует, чтобы x было положительным. Квадратная функция определяется уравнением f ( x ) = x 2, на этот раз нет ограничения для х .

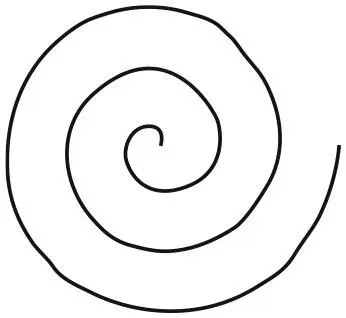
Архимедова спираль

Мы можем геометрически изобразить функцию, определяя координату y по заданному уравнению для x: y = f ( x ). Это уравнение задает отношение между двумя координатами и таким образом определяет форму кривой. Такая кривая называется графиком функции f .

На развитие математики заметно повлияло швейцарское семейство Бернулли. На протяжении четырех поколений из него выходили выдающиеся математики, поражавшие своим талантом. Часто называемые математической мафией, Бернулли обычно начинали свою карьеру в качестве слуг закона, медицины или церкви, но рано или поздно возвращались к главному призванию – математике, на профессиональном или любительском уровне.

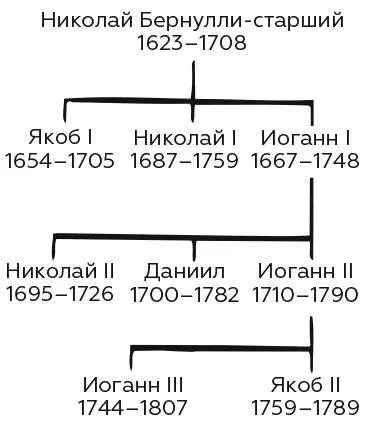
Якоб I (1654–1705)

Изобрел полярные координаты, формулу для радиуса кривизны плоской кривой. Изучил специальные кривые, такие как цепная линия и лемниската. Вывел доказательство, что изохрона (кривая, по которой тяжелая точка опускается за равные промежутки времени на равные вертикальные отрезки) является перевернутой циклоидой. Изучал изопериметрические фигуры, имеющие кратчайшую длину при различных условиях; позже это привело к развитию вариационного исчисления. Один из первых исследователей теории вероятностей и автор первой книги на эту тему, «Искусство предположений» («Ars conjectandi»). Якоб завещал выгравировать на своей могиле логарифмическую спираль и надпись на латыни: «Eadem mutata resurgo» («Измененная, я вновь воскресаю»).

Иоганн I (1667–1748)

Ввел новые способы счисления и распространил их в Европе. Маркиз де Лопиталь опубликовал труды Иоганна в своем первом учебнике по исчислению (точное название «Анализ бесконечно малых»). Правило Лопиталя для нахождения пределов, раскрывающих неопределенности вида 0/0, – заслуга Иоганна. Написал труды по оптике (отражение и рефракция), об ортогональных траекториях семейства кривых, длинах кривых и нахождении площадей с помощью интегрального исчисления, по аналитической тригонометрии и экспоненциальным функциям. Вычислил брахистохрону (кривую скорейшего спуска) и длину циклоиды.