Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

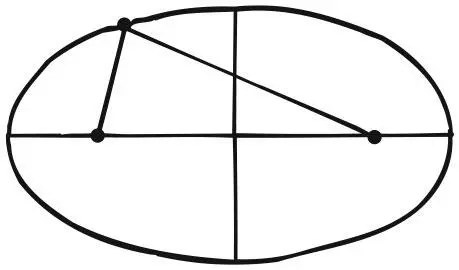
Свойства фокусов эллипса

Геометрическое место точек (ГМТ) определяет геометрическую фигуру как множество точек на плоскости или в пространстве, обладающих некоторым свойством. Например, мы можем искать ГМТ, сумма расстояний от которых до двух заданных точек есть величина постоянная. Это эллипс с двумя фокусами. Это свойство эллипса было известно еще древним грекам.

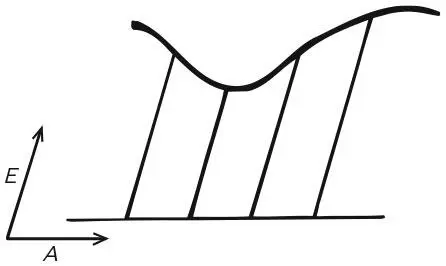
Подход Ферма к координатам

Ферма же обратил внимание на принцип: если условия, налагаемые на точку, можно выразить в виде одного уравнения с двумя неизвестными, соответствующее ГМТ будет кривой – или прямой линией, которую мы будем рассматривать как определенный тип кривой во избежание ненужных расхождений.

Он иллюстрировал этот принцип схемой, на которой две неизвестных величины A и E представлены как расстояния в двух разных направлениях.

Затем он составил несколько отдельных уравнений, связующих А и Е , и объяснил, какие кривые они представляют. Например, если А 2= 1 + Е 2, то ГМТ является гиперболой.

Ферма ввел косоугольную систему координат на плоскости (косвенно подразумевая, что этот угол не обязательно должен быть прямым). Переменные А и Е – две координаты , которые мы называем x и y , для любой точки относительно данных осей. Итак, принцип Ферма убедительно утверждает, что любое уравнение с двумя переменными представляет кривую, и его примеры показывают нам, какое уравнение представляет какую кривую из перечня основных кривых, составленного греками.

Современное представление о системе координат сложилось в трудах Декарта. В повседневной жизни мы сталкиваемся с двумерными и трехмерными пространствами, и нам нужна вся сила воображения, чтобы представить себе что-то более сложное. Наша зрительная система отображает внешний мир как двумерную картинку для каждого глаза – подобно той, что мы видим на экране телевизора. Мелкие различия в изображениях от каждого глаза наш мозг комбинирует и интерпретирует в ощущение глубины изображения, и мы получаем возможность воспринимать окружающий мир как трехмерное пространство.

Ключом к представлению о многомерных пространствах является идея системы координат, представленная Декартом в виде приложения «Геометрия» к его труду «Рассуждение о методе». Его идея состояла в том, что геометрия на плоскости может быть представлена в алгебраических выражениях. Его подход аналогичен методу Ферма. Выберите точку на плоскости и назовите ее начальной. Проведите две оси – линии, проходящие через начальную точку и пересекающиеся под прямым углом. Обозначьте одну ось как x , другую – y . Тогда любая точка P плоскости будет определяться парой расстояний ( x, y ), которые говорят нам о том, как далеко находится эта точка от начала, если измерять соответствующие перпендикуляры от точки P до осей x и y . Например, на карте x может обозначать расстояние к востоку от начальной точки (с отрицательными числами, представляющими направление на запад), а y – расстояние к северу от исходной точки (с отрицательными показателями, представляющими направление на юг).

Декарт начализучать математику в 1618 г., став учеником голландского ученого Исаака Бекмана. Он покинул Голландию и путешествовал по Европе, пока в 1619 г. не вступил в баварскую армию. Он продолжал путешествовать с 1620 по 1628 г., побывал в Богемии, Венгрии, Германии, Голландии, Франции и Италии. В Париже в 1622 г. он познакомился с Мареном Мерсенном и с тех пор регулярно переписывался с ним, что позволяло ему постоянно быть в курсе последних достижений ведущих научных школ.

В 1628 г. Декарт осел в Голландии и начал свой первый труд «Мир» (Le Monde), в частности «Трактат о свете», описывавший свойства света. Когда Декарту стало известно о домашнем аресте Галилео Галилея, он испугался и задержал публикацию книги. Только после его смерти работа была издана в усеченном виде. Он продолжил развивать свои идеи о логическом мышлении в большом труде, изданном в 1637 г., «Рассуждение о методе…». У книги было три приложения: «Диоптрика», «Метеоры» и «Геометрия».

Самая его амбициозная книга, «Первоначала философии», увидела свет в 1644 г. Она делилась на четыре части: «Об основах человеческого познания», «О началах материальных вещей», «О видимом мире» и «О земле». Это была попытка подвести единый математический фундамент под всеобъемлющую физическую Вселенную, преобразуя все естественные составляющие в механические объекты.

В 1649 г. Декарт отправилсяв Швецию, чтобы занять место наставника при королеве Кристине. Королева оказалась ранней пташкой, а Декарт не имел привычки подниматься раньше 11 часов. Необходимость вести уроки математики в пять утра, да еще в холодном сыром климате, подорвала здоровье Декарта. Через несколько месяцев он скончался от пневмонии.

Координаты работают и в трехмерном пространстве, но здесь двух значений уже недостаточно для локализации точки. А вот три достаточно. Кроме направления восток – запад или север – юг нам необходима еще и точка выше или ниже начальной. Обычно для расстояний выше нее мы используем положительное число, ниже – отрицательное. Координаты в пространстве обозначаются ( x, y, z ).

Поэтому плоскость называют двумерной, а пространство трехмерным. Число измерений зависит от того, сколько чисел нам необходимо для описания данной точки.

В трехмерном пространстве отдельное уравнение, содержащее x, y и z , обычно определяет поверхность. Например, x 2+ y 2+ z 2= 1 утверждает, что точка ( x, y, z ) всегда расположена на расстоянии в одну единицу от начальной точки. Это позволяет предположить, что она лежит на единичной сфере с центром в начальной точке.

Обратите внимание, что слово «мера» применяется здесь не в буквальном значении. Мы не пытаемся найти количество измерений пространства через что-то, называемое мерой, чтобы затем подсчитать ее. Мы определяем, сколько чисел необходимо, чтобы определить положение в пространстве, – это и будет размерностью.

Нам легче будет понять, как развивалась координатная геометрия, если познакомимся с тем, как работает современная система. Существует несколько вариантов, но все они основаны на том, что для начала на плоскость наносят две линии под названием оси . Точка их пересечения, общая точка, – начальная точка . Как правило, соблюдается такое условие: одна ось – горизонтальная, другая – вертикальная.